题目内容
下列命题:
①若方程ax2+bx+c=0有一根为-
,则方程必有两相等的实数根;
②若b>a+c,则一元二次方程ax2+bx+c=0有两个不相等的实数根;
③若b=2a+3c,则一元二次方程ax2+bx+c=0有两个不相等的实数根;
④若关于x的一元二次方程ax2+bx+c=0有一根为0,则c=0
其中正确的是( )
①若方程ax2+bx+c=0有一根为-
| b |
| 2a |
②若b>a+c,则一元二次方程ax2+bx+c=0有两个不相等的实数根;
③若b=2a+3c,则一元二次方程ax2+bx+c=0有两个不相等的实数根;
④若关于x的一元二次方程ax2+bx+c=0有一根为0,则c=0
其中正确的是( )
| A、只有①②③ |
| B、只有①③④ |
| C、只有①②④ |
| D、只有②③④ |
考点:根的判别式,一元二次方程的解
专题:
分析:通过计算判别式的值对①③进行判断;
利用特例对②进行判断;
根据方程解的定义对④进行判断.
利用特例对②进行判断;
根据方程解的定义对④进行判断.
解答:解:①若方程ax2+bx+c=0有一根为-
,则a×(-
)2+b×(-
)+c=0,即
=0,所以4ac-b2=0,那么△=b2-4ac=0,方程必有两相等的实数根,所以①正确;
②若b>a+c,设a=-4,b=10,c=-9,则△<0,一元二次方程ax2+bx+c=0没有实数根,所以②错误;
③若b=2a+3c,则△=b2-4ac=4(a+c)2+5c2>0,一元二次方程ax2+bx+c=0有两个不相等的实数根,所以③正确;
④若关于x的一元二次方程ax2+bx+c=0有一根为0,则a×02+b×0+c=0,即c=0,所以④正确.
故选B.
| b |
| 2a |
| b |
| 2a |
| b |
| 2a |
| b2-2b2+4ac |
| 4a |
②若b>a+c,设a=-4,b=10,c=-9,则△<0,一元二次方程ax2+bx+c=0没有实数根,所以②错误;
③若b=2a+3c,则△=b2-4ac=4(a+c)2+5c2>0,一元二次方程ax2+bx+c=0有两个不相等的实数根,所以③正确;
④若关于x的一元二次方程ax2+bx+c=0有一根为0,则a×02+b×0+c=0,即c=0,所以④正确.
故选B.
点评:本题考查了根的判别式,利用一元二次方程根的判别式(△=b2-4ac)判断方程的根的情况.
一元二次方程ax2+bx+c=0(a≠0)的根与△=b2-4ac有如下关系:
①当△>0时,方程有两个不相等的两个实数根;
②当△=0时,方程有两个相等的两个实数根;
③当△<0时,方程无实数根.
同时考查了一元二次方程的解的定义.
一元二次方程ax2+bx+c=0(a≠0)的根与△=b2-4ac有如下关系:
①当△>0时,方程有两个不相等的两个实数根;
②当△=0时,方程有两个相等的两个实数根;
③当△<0时,方程无实数根.
同时考查了一元二次方程的解的定义.

练习册系列答案
 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案
相关题目
以下五家银行行标中,是轴对称图形的有( )


| A、1个 | B、2个 | C、3个 | D、4个 |
下列说法正确的是( )
| A、有理数的绝对值为正数 |
| B、如果两数之和为0,则这两个数的绝对值相等 |
| C、只有正数或负数才有相反数 |
| D、任何数都有倒数 |
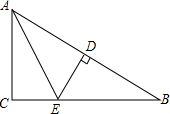 如图所示,在△ABC中,AC⊥BC,AE为∠BAC的平分线,DE⊥AB,AB=7cm,AC=3cm,则BD等于( )
如图所示,在△ABC中,AC⊥BC,AE为∠BAC的平分线,DE⊥AB,AB=7cm,AC=3cm,则BD等于( )| A、1cm | B、2cm |
| C、3cm | D、4cm |