题目内容
如图,以BC为直径的圆0交∆CFB的边CF于点A,BM平分∠ABC交AC于点M,AD⊥BC于点D,AD交BM于点N,ME⊥BC于点E,AB2 =AF.AC.
【小题1】求△ANM?△ENM;
【小题2】求证:FB是圆O的切线
【小题3】证明四边形AMEN是菱形.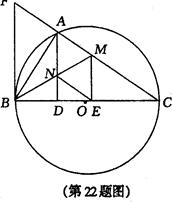
【小题1】证明:因为BC是圆0的直径,
所以:∠BAC=900 (1分)
又EM⊥BC,BM平分∠ABC,
所以:AM="ME." ∠AMN=∠EMN
又MN=MN
所以:∆ANM?∆ENM
【小题2】因为:AB2=AF?AC,

又∠ABF=∠C
所以:∆ABF~∆ACB (4分)
所以:∠ABF=∠C
又∠FBC="∠ABC+∠FBA=" 900,
.’.FB是圆O的切线
【小题3】解:由(1)得AN="EN,AM=EM," ∠AMN=∠EMN
又:AN//ME
所以:∠ANM=∠EMN (7分)
所以:∠AMN=∠ANM (8分)
所以:AN=AM
AM=ME+EN=AN
所以:四边形AMEN是菱形 (10分)
解析

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
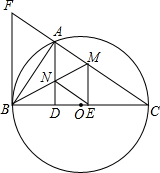 如图,以BC为直径的⊙O交△CFB的边CF于点A,BM平分∠ABC交AC于点M,AD⊥BC于点D,AD交BM于点N,ME⊥BC于点E,AB2=AF•AC,cos∠ABD=
如图,以BC为直径的⊙O交△CFB的边CF于点A,BM平分∠ABC交AC于点M,AD⊥BC于点D,AD交BM于点N,ME⊥BC于点E,AB2=AF•AC,cos∠ABD= (2012•浦口区一模)如图,以BC为直径的⊙O与△ABC的另两边分别相交于点D、E.若∠A=70°,BC=2,则图中阴影部分面积为
(2012•浦口区一模)如图,以BC为直径的⊙O与△ABC的另两边分别相交于点D、E.若∠A=70°,BC=2,则图中阴影部分面积为 (2013•澄海区模拟)如图,以BC为直径的⊙O与△ABC的另两边分别相交于点D、E.若∠A=60°,BC=2,则图中阴影部分的面积为
(2013•澄海区模拟)如图,以BC为直径的⊙O与△ABC的另两边分别相交于点D、E.若∠A=60°,BC=2,则图中阴影部分的面积为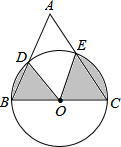 (2013•眉山)如图,以BC为直径的⊙O与△ABC的另两边分别相交于点D、E.若∠A=60°,BC=4,则图中阴影部分的面积为
(2013•眉山)如图,以BC为直径的⊙O与△ABC的另两边分别相交于点D、E.若∠A=60°,BC=4,则图中阴影部分的面积为 (2012•攀枝花)如图,以BC为直径的⊙O1与⊙O2外切,⊙O1与⊙O2的外公切线交于点D,且∠ADC=60°,过B点的⊙O1的切线交其中一条外公切线于点A.若⊙O2的面积为π,则四边形ABCD的面积是
(2012•攀枝花)如图,以BC为直径的⊙O1与⊙O2外切,⊙O1与⊙O2的外公切线交于点D,且∠ADC=60°,过B点的⊙O1的切线交其中一条外公切线于点A.若⊙O2的面积为π,则四边形ABCD的面积是