题目内容
【题目】如图,等边△ABC的边长为10cm,点D从点C出发沿CA向点A运动,点E从点B出发沿AB的延长线BF向右运动,已知点D,E都以1cm/s的速度同时开始运动,运动过程中DE与BC相交于点P,点D运动到点A后两点同时停止运动.
(1)当△ADE是直角三角形时,求D,E两点运动的时间;
(2)求证:在运动过程中,点P始终是线段DE的中点.

【答案】(1)![]() s;(2)证明见解析
s;(2)证明见解析
【解析】
(1)经过分析当△ADE是直角三角形时,只有∠ADE=90°的情况,此时∠AED=30°.用运动时间t表示出AD和AE,根据30度直角三角形的性质构造关于t的方程即可求解;
(2)过D点作DK∥AB交BC于点K,证明△DKP≌△EBP即可说明点P始终是线段DE的中点.
(1)当△ADE是直角三角形时,只有∠ADE=90°的情况,
∵∠A=60°,
∴∠AED=30°,
∴AE=2AD,
设D点运动时间为t,则E点运动时间也为t,
∴AD=10﹣t,AE=10+t,
∴10+t=2(10﹣t),解得t=![]() ,
,
所以当△ADE是直角三角形时,D,E两点运动的时间为![]() 秒;
秒;
(2)过点D作DK∥AB交BC于点K,
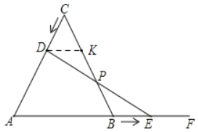
∵△ABC是等边三角形,
∴∠C=∠CDK=∠CKD=60°,
∴CD=DK=CK,∠DKP=∠EBP=120°,
设D、E运动时间为t秒,则CD=BE=t,
在△DKP和△EBP中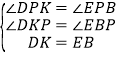 ,
,
∴△DKP≌△EBP(AAS),
∴PD=PE,
所以P始终为DE中点.

练习册系列答案
相关题目