��Ŀ����
����Ŀ����ͼ����֪��![]() �����κ���
�����κ���![]() �ĶԳ���Ϊֱ��
�ĶԳ���Ϊֱ��![]() ����ͼ�����
����ͼ�����![]() ��
��![]() �ύ����һ��
�ύ����һ��![]() ����
����![]() �ύ�ڵ�
�ύ�ڵ�![]() .
.
��1������κ����Ľ���ʽ��д���������ꣻ
��2������![]() ͬʱ��
ͬʱ��![]() �����������ÿ��2����λ���ȵ��ٶȷֱ���
�����������ÿ��2����λ���ȵ��ٶȷֱ���![]() ��
��![]() �����˶��������˶���ʱ��Ϊ
�����˶��������˶���ʱ��Ϊ![]() �룬������һ���㵽���յ�ʱ����һ����Ҳ��ֹ֮ͣ�˶�������
�룬������һ���㵽���յ�ʱ����һ����Ҳ��ֹ֮ͣ�˶�������![]() ����
����![]() ��
��![]() ���ۣ�����
���ۣ�����![]() ǡ�������������ϵ�
ǡ�������������ϵ�![]() ��������
��������![]() ��ֵ����
��ֵ����![]() �����ꣻ
�����ꣻ
��3���ڣ�2���������£�QΪBN���е㣬��̽�����������Ƿ���ڵ�![]() ��ʹ����
��ʹ����![]() Ϊ�������������
Ϊ�������������![]() ���ƣ�������ڣ��������
���ƣ�������ڣ��������![]() �����ꣻ��������ڣ���˵������.
�����ꣻ��������ڣ���˵������.
���𰸡���1��![]() ����������Ϊ
����������Ϊ ����2��
����2��![]() ��
�� ![]() ����3�����ڣ�
����3�����ڣ� ![]() ��
�� ![]() ��
��  .
.
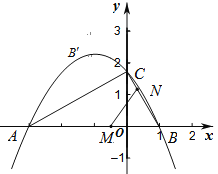
����������1���������߶Գ���Ϊ-1��������A(3,0)�����a��b,�Ӷ���������߽���ʽ�Ͷ�������.
(2)��A,B,C����ɵó���CBA=60������BM=BN�Ƴ���MBN����������,���ۺ��BMN��![]() �Ƴ�
�Ƴ�![]() M��MB�Ӷ��õ�
M��MB�Ӷ��õ�![]() ��1-3t,
��1-3t, ![]() t��,��
t��,��![]() ���뼴����⡣
���뼴����⡣
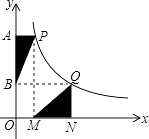
��3��������������۵�P�Ĵ����ԣ�����P��x���ϣ��͵�P��y����.
��:(1)������ã�  ����ã�
����ã� 

![]() ���κ����Ľ���ʽΪ
���κ����Ľ���ʽΪ![]()
![]() ,�䶥������Ϊ
,�䶥������Ϊ .
.
(2)������֪�� ![]() ,
, ![]()
![]()
��![]()
![]() ,
,![]() ��
��![]() ����������.
����������. ![]() .
.
��![]() ��
��![]() ���ۺ�
���ۺ� ![]() ,
,
![]()
![]()
![]() .
.

����![]() ���������ϣ�����
���������ϣ�����![]()
����ã� ![]() ��
�� ![]() .
.
��ʱ�� ![]() ��
�� ![]() .
.
��3��������ɵ�![]() Ϊֱ�������Σ�
Ϊֱ�������Σ�
��![]() ��
�� .
.
�ֶ���������ۣ�
1),��![]() ��
��![]() ����ʱ����
����ʱ����![]() ��
��![]() ����
����![]() ,��
,��![]() ,��ʱ
,��ʱ![]() ; ��
; ��![]() ��
��![]() ����
����![]() ,��
,��![]() ,��ʱ
,��ʱ![]() ;
; ![]() ��
��![]() ��������λ��ʱ��������
��������λ��ʱ��������![]() ��Ϊֱ�������Σ���������
��Ϊֱ�������Σ���������![]() ����.
����.
2),ͬ������![]() ����y����ʱ,��
����y����ʱ,��![]() ����
����![]() ����
����![]() ����ʱ
����ʱ ;��
;��![]() ��
��![]() ��y����
��y����![]() ,��
,��![]() ��
��![]() �����ƣ�
�����ƣ� ![]() ��
��![]() ��������λ��ʱ��������
��������λ��ʱ��������![]() ��Ϊֱ�������Σ���������
��Ϊֱ�������Σ���������![]() ����.
����.

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�