题目内容
 △ABC称为第一个三角形,其周长为1,连接△ABC各边的中点,所组成的△DEF为第二个三角形,其周长为
△ABC称为第一个三角形,其周长为1,连接△ABC各边的中点,所组成的△DEF为第二个三角形,其周长为 ,依此类推,第2000个三角形周长为
,依此类推,第2000个三角形周长为
- A.

- B.
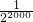
- C.

- D.

C
分析:分别写出所得三角形的周长,然后可发现结果的次数与个数差1,从而可求.
解答:第一个三角形,△ABC的周长=1,
第二个三角形的周长等于 ,
,
第三个三角形的周长等于( )2,
)2,
第四个三角形的周长等于( )3,
)3,
…,
所以第2000个三角形的周长等于( )2000-1=(
)2000-1=( )1999=
)1999= .
.
故选C.
点评:本题考查了三角形中位线定理.关键是找出结果的次数与个数的关系.
分析:分别写出所得三角形的周长,然后可发现结果的次数与个数差1,从而可求.
解答:第一个三角形,△ABC的周长=1,

第二个三角形的周长等于
 ,
,第三个三角形的周长等于(
 )2,
)2,第四个三角形的周长等于(
 )3,
)3,…,
所以第2000个三角形的周长等于(
 )2000-1=(
)2000-1=( )1999=
)1999= .
.故选C.
点评:本题考查了三角形中位线定理.关键是找出结果的次数与个数的关系.

练习册系列答案
 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目



