äãá¢áÖàï
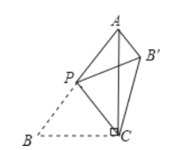
Àƒäãá¢À¢ØîøˆÈ˜àÓë¥È˜éæöÿüÔyȧax2ȨbxȨc (aÀì0)çáÑËçÐöˆM (1Ș9), ƒÙ¿»éæöÿüÔèüçáê§çÐA(ÈÙ3ȘÈÙ7)¤ëB (3, m)çáøÝüÔ§£éæöÿüÔçáÑå°óøÃÆÖçÐCÈÛ

(1)úµéæöÿüÔçá§ãö—ò§¤ëøÝüÔABçá§ãö—ò§È£
(2)åÖéæöÿüÔèüòúñþÇÌåÖçÐDȘò¿çûSÀ¼DACȧ2SÀ¼DCM?à¶ÇÌåÖȘúµ°—çÐDçáæ½ÝõÈ£à¶ý£ÇÌåÖȘúŠùçû¼âÚÆèÈÛ
(3)à¶çÐPåÖéæöÿüÔèüȘçÐQåÖxøÃèüȘçÝØåçÐAÀÂMÀÂPÀÂQöˆÑËçÐçáùáÝÔÅöòúó§ÅÅùáÝÔÅöòÝȘøݧÆÅÇ°—ôºæÐæÐä¾¥±çáçÐPçáæ½ÝõÈÛ
ÀƒÇÞ¯¡À¢È´1ÈˋéæöÿüÔçáÝÚÇÿò§öˆÈ¤![]() ȘøÝüÔ
ȘøÝüÔ![]() çáÝÚÇÿò§öˆÈ¤
çáÝÚÇÿò§öˆÈ¤![]() ȣȴ2ÈˋçÐD
ȣȴ2ÈˋçÐD![]() £·
£·![]() ȣȴ3ÈˋçÐ
ȣȴ3ÈˋçÐ![]() £·
£·![]() £·
£·![]() Ș
Ș![]() £·
£·![]() Ș
Ș![]() ÈÛ
ÈÛ
Àƒ§ãö—À¢
È´1ÈˋèÒѱÇö¤₤ò»ÝÚÇÿò§öˆÈ¤![]() Șâ«ÆûÑËçÐò§¥Ç¢èúµ§ãÈ£
Șâ«ÆûÑËçÐò§¥Ç¢èúµ§ãÈ£
È´2ÈˋàÓë¥È˜èÒçÐ![]() ȘçÐ
ȘçÐ![]() ȘÝÚòƒ°—DHȘMC°ÊÑàȘ¡ªƒï
ȘÝÚòƒ°—DHȘMC°ÊÑàȘ¡ªƒï![]() ȘêÅñ§°äúµ§ã¥Ç¢èÈ£
ȘêÅñ§°äúµ§ã¥Ç¢èÈ£
È´3Èˋñø![]() òúó§ÅÅùáÝÔÅöçáØ£ä¾ÝÔÀÂ
òúó§ÅÅùáÝÔÅöçáØ£ä¾ÝÔÀÂ![]() òúó§ÅÅùáÝÔÅöçáÑå§úüÔê§øøúÕ¢—ȘñøÝÞúµ§ã¥Ç¢èÈÛ
òúó§ÅÅùáÝÔÅöçáÑå§úüÔê§øøúÕ¢—ȘñøÝÞúµ§ã¥Ç¢èÈÛ
§ãȤȴ1ÈˋÀÔéæöÿüÔyȧax2ȨbxȨc (aÀì0)çáÑËçÐöˆM (1Ș9)Ș
ÀÁèÒѱÇö¤₤ò»§ãö—ò§öˆÈ¤![]() Ș
Ș
ÀÔA(ÈÙ3ȘÈÙ7)åÖéæöÿüÔèüȘ
ÀÁ![]() Ș
Ș
§ãçûȤ![]() Ș
Ș
¿òéæöÿüÔçáÝÚÇÿò§öˆÈ¤![]() Ș
Ș
ÀÔB (3, m)åÖéæöÿüÔèüȘ
ùªØå![]()
ÀÁçÐBçáæ½Ýõöˆ![]() Ș
Ș
èÒøÝüÔAB§ãö—ò§öˆ![]() Ș
Ș
ÀÁ![]() Ș
Ș
§ãçû![]() Ș
Ș
ÀÁøÝüÔ![]() çáÝÚÇÿò§öˆÈ¤
çáÝÚÇÿò§öˆÈ¤![]() È£
È£
È´2ÈˋÇÌåÖȘâÚÆèȤ
ÆèѱÇö¤₤ò»![]() çûÑå°óøÃöˆÈ¤
çûÑå°óøÃöˆÈ¤![]() Șå·çÐ
Șå·çÐ![]() Ș
Ș
¿»çÐ![]() æ¼
æ¼![]() øÃçáó§ÅÅüÔ§£
øÃçáó§ÅÅüÔ§£![]() ÆÖçÐ
ÆÖçÐ![]() Ș
Ș

èÒçÐ![]() ȘçÐ
ȘçÐ![]() Ș
Ș
ÀÁDH=![]() ȘMC=9-1=8Ș
ȘMC=9-1=8Ș
![]() Ș
Ș
å·![]() Ș
Ș
§ãçûȤ![]() £·5Ș
£·5Ș
¿òçÐD![]() £·
£·![]() È£
È£
È´3ÈˋèÒçÐ![]() ÀÂçÐ
ÀÂçÐ![]() Ș
Ș![]() Ș
Ș
ÂìçÝ![]() òúó§ÅÅùáÝÔÅöçáØ£ä¾ÝÔòÝȘ
òúó§ÅÅùáÝÔÅöçáØ£ä¾ÝÔòÝȘ
çÐ![]() ü·æµó§Øó4¡—çËö£ü·üôó§Øó16¡—çËö£çûç§
ü·æµó§Øó4¡—çËö£ü·üôó§Øó16¡—çËö£çûç§![]() Ș
Ș
ÀÁçÐ![]() ü·æµó§Øó4¡—çËö£ü·üôó§Øó16¡—çËö£çûç§çÐ
ü·æµó§Øó4¡—çËö£ü·üôó§Øó16¡—çËö£çûç§çÐ![]() Ș
Ș
ÀÁt=-16,
å·![]() Ș
Ș
§ãçûȤ![]() £·
£·![]() Ș
Ș
¿òçÐ![]() £·
£·![]() È£
È£
ÂÖçÝ![]() òúó§ÅÅùáÝÔÅöçáÑå§úüÔòÝȘ
òúó§ÅÅùáÝÔÅöçáÑå§úüÔòÝȘ
ÆèøÅçп¨ò§çûȤ![]() Ș
Ș![]() Ș
Ș
ÀÔ![]() Ș
Ș
ÀÁ![]()
§ãçûȤ![]() Ș
Ș
¿òçÐ![]() Ș
Ș![]() £·
£·![]() Ș
Ș![]() ȣ
È£
æÜèüȘçÐ![]() £·
£·![]() £·
£·![]() Ș
Ș![]() £·
£·![]() Ș
Ș![]() ÈÛ
ÈÛ

 Ø£ƒÚ¡ÐÑ´üçêÅÇÞ¯¡
Ø£ƒÚ¡ÐÑ´üçêÅÇÞ¯¡ û«ÅÈæ¼Øç݃üçêÅÇÞ¯¡
û«ÅÈæ¼Øç݃üçêÅÇÞ¯¡ úÃúèÑÿÖøÉýãåô¢¥øÝë´û«ÅÈüçêÅÇÞ¯¡
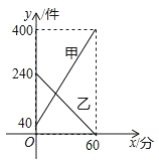
úÃúèÑÿÖøÉýãåô¢¥øÝë´û«ÅÈüçêÅÇÞ¯¡Àƒäãá¢À¢á°øøÅë¤éçáçÓààùÛó¼¿Ê漿»°äàÓüôȤåÖ§Æë´çÓåÇØ夵ȘÇÆ°¾ò¥öôÑà20![]() üô¥ÆààùÛüðøÅçáùÛȘçÝùÛöôÇÿç§èÒÑ´öôÑà60
üô¥ÆààùÛüðøÅçáùÛȘçÝùÛöôÇÿç§èÒÑ´öôÑà60![]() òÝȘ¥ÆààëÈø¿È£Çù¤µùÛüðøÅçáùÛöô¢ˆò¥øÞ§Ëüô§çȘçÝüô§çç§ÝÈöôöôÑà30
òÝȘ¥ÆààëÈø¿È£Çù¤µùÛüðøÅçáùÛöô¢ˆò¥øÞ§Ëüô§çȘçÝüô§çç§ÝÈöôöôÑà30![]() òÝȘåìÇöæåÑ₤¥ÆààùÛüðøÅçáùÛøê60
òÝȘåìÇöæåÑ₤¥ÆààùÛüðøÅçáùÛøê60![]() Ș¥ÆààëÈø¿È£çÝùÛüðøÅçáùÛöôüô§çç§30
Ș¥ÆààëÈø¿È£çÝùÛüðøÅçáùÛöôüô§çç§30![]() òÝȘåìÇöæåÑ₤¥ÆààȘÀÙÀÙȘ¯ÇííØåèüñ§ò§ý£ÑüîÙ£ñÈÛÅÀÆŸ¡ªƒïîÏü¯¤₤ò»çáƒÙîÕȘÑå¡ûÅë¤éçÓààùÛó¼ùÛüðøÅçáùÛöôùÌòÝ¥ðÝð£₤çá¿Ìô觽ÅÅêù䧃¢È˜ñÂüøùÛöô
òÝȘåìÇöæåÑ₤¥ÆààȘÀÙÀÙȘ¯ÇííØåèüñ§ò§ý£ÑüîÙ£ñÈÛÅÀÆŸ¡ªƒïîÏü¯¤₤ò»çáƒÙîÕȘÑå¡ûÅë¤éçÓààùÛó¼ùÛüðøÅçáùÛöôùÌòÝ¥ðÝð£₤çá¿Ìô觽ÅÅêù䧃¢È˜ñÂüøùÛöô![]() òúòÝ¥ð
òúòÝ¥ð![]() çá¤₤ò»È˜óðøÅ
çá¤₤ò»È˜óðøÅ![]() È´çËö£È¤
È´çËö£È¤![]() ÈˋÝÚòƒùÛüðøÅùÛçáöôÑàȘ
ÈˋÝÚòƒùÛüðøÅùÛçáöôÑàȘ![]() È´çËö£È¤
È´çËö£È¤![]() ÈˋÝÚòƒ§Æë´çÓåǤµçáòÝ¥ðÈÛüôûÌòúÅÀÆŸçá䧃¢¿»°äȘúŠý¿°ðëõí«È¤
ÈˋÝÚòƒ§Æë´çÓåǤµçáòÝ¥ðÈÛüôûÌòúÅÀÆŸçá䧃¢¿»°äȘúŠý¿°ðëõí«È¤
È´1ÈˋÅÀÆŸ¥úô¥êùÇÆ°¾ò¥öôÑà20![]() çÖØ£Çö¥ÆààøêèÒÑ´öôÑà60
çÖØ£Çö¥ÆààøêèÒÑ´öôÑà60![]() ȘøÛ¤µùÛöôâðàÇøêÝÈöôöôÑà30
ȘøÛ¤µùÛöôâðàÇøêÝÈöôöôÑà30![]() çá¿»°äøÅȘ
çá¿»°äøÅȘ![]() ùÌ
ùÌ![]() çáÝð£₤úÕ¢—ȘàÓüôÝÚùªòƒÈ¤
çáÝð£₤úÕ¢—ȘàÓüôÝÚùªòƒÈ¤
§Æë´çÓåǤµçáòÝ¥ð | 0 | 2 | 4 | 8 | 10 | 12 | 14 | 16 | 18 | 20 | ÀÙ |
ùÛüðøÅùÛçáöôÑà | 20 | 30 | 40 | 60 | 51 | 45 | 40 | 36 | 33 | 30 |
ÂìúŠÅÇ°—Ø£¡—ñ«¤ü¥Æàà§æÑö![]() ÆŠ
ÆŠ![]() ¿Äüççá¤₤ò»§ãö—ò§______________È£
¿Äüççá¤₤ò»§ãö—ò§______________È£
ÂÖ¡ªƒï¡ûçÓààùÛó¼çá¿Êæ¼äÄçÐȘçÝçÖѱÇö¥ÆààøêèÒÑ´öôÑà60![]() òÝȘƒÁ⊧Æë´çÓåÇçáòÝ¥ð
òÝȘƒÁ⊧Æë´çÓåÇçáòÝ¥ð![]() öˆ________
öˆ________![]() ÈÛ
ÈÛ
È´2Èˋ¡ªƒïèüò—çáÝÚ¡þȘÅÀÆŸ£Ù°—êùçÝ![]() òÝçá¤₤ò»ë¥üµÈ˜úŠ¡ªƒï¡ûçÓààùÛó¼çá¿Êæ¼äÄçÐȘ¯ÿù«£Ù°—çÝ
òÝçá¤₤ò»ë¥üµÈ˜úŠ¡ªƒï¡ûçÓààùÛó¼çá¿Êæ¼äÄçÐȘ¯ÿù«£Ù°—çÝ![]() òÝçá¤₤ò»ë¥üµÈÛ
òÝçá¤₤ò»ë¥üµÈÛ
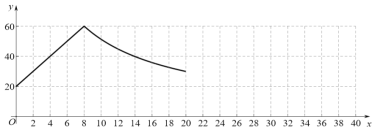
È´3ÈˋØîøˆòòØùàùäÍÐÍåÀçáùÛöôå¥öˆ![]() ȘÅÀÆŸåÖèüöÓ8çÐí«§Æë´çÓåÇȘùÛüðøÅùÛöôöˆ20
ȘÅÀÆŸåÖèüöÓ8çÐí«§Æë´çÓåÇȘùÛüðøÅùÛöôöˆ20![]() ȘààùÛ󼢈ò¥¯Çèüò—áÈò§¿Êæ¼È˜à¶ý£¢¥ôúóðù«Ø·ùÄçáƯüšÈ˜úŠöòåÖèüöÓ9çÐ30ñøòÝȘààùÛó¼çáùÛöô______È´äŸÀ¯òúÀÝ£·À¯ñþÀÝÈˋòò¤üù«ÐÍåÀȘâÚÆèòú_________________ÈÛ
ȘààùÛ󼢈ò¥¯Çèüò—áÈò§¿Êæ¼È˜à¶ý£¢¥ôúóðù«Ø·ùÄçáƯüšÈ˜úŠöòåÖèüöÓ9çÐ30ñøòÝȘààùÛó¼çáùÛöô______È´äŸÀ¯òúÀÝ£·À¯ñþÀÝÈˋòò¤üù«ÐÍåÀȘâÚÆèòú_________________ÈÛ