题目内容
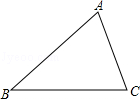
△ABC为等边三角形,边长为a,DF⊥AB,EF⊥AC,
(1)求证:△BDF∽△CEF;
(2)若a=4,设BF=m,四边形ADFE面积为S,求出S与m之间的函数关系,并探究当m为何值时S取最大值;
(3)已知A、D、F、E四点共圆,已知tan∠EDF=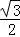 ,求此圆直径.
,求此圆直径.
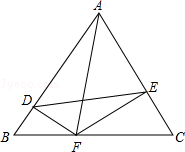
(1)求证:△BDF∽△CEF;
(2)若a=4,设BF=m,四边形ADFE面积为S,求出S与m之间的函数关系,并探究当m为何值时S取最大值;
(3)已知A、D、F、E四点共圆,已知tan∠EDF=
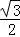 ,求此圆直径.
,求此圆直径.
(1)证明见解析
(2)S与m之间的函数关系为:S═﹣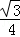 (m﹣2)2+3
(m﹣2)2+3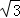 (其中0<m<4).当m=2时,S取到最大值,最大值为3
(其中0<m<4).当m=2时,S取到最大值,最大值为3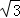
(3)此圆直径长为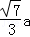 .
.
(2)S与m之间的函数关系为:S═﹣
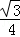 (m﹣2)2+3
(m﹣2)2+3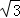 (其中0<m<4).当m=2时,S取到最大值,最大值为3
(其中0<m<4).当m=2时,S取到最大值,最大值为3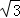
(3)此圆直径长为
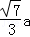 .
.试题分析:(1)由已知可知∠BDF=∠CEF,∠B=∠C,所以得证.
(2)四边形ADFE面积S可以看成△ADF与△AEF的面积之和,这两个三角形均为直角三角形,在△BDF与△CEF中,由三角函数可以用m表示出BD、DF、CE、EF的长,进而可得AD、AE的长,从而可以用含m的代数式表示S,然后通过配方,转化为二次函数的最值问题,就可以解决问题.
(3)由已知易知AF就是圆的直径,利用圆周角定理将∠EDF转化为∠EAF.在△AFC中,知道tan∠EAF、∠C、AC,通过解直角三角形就可求出AF长.
试题解析:(1):∵DF⊥AB,EF⊥AC,
∴∠BDF=∠CEF=90°.
∵△ABC为等边三角形,
∴∠B=∠C=60°.
∵∠BDF=∠CEF,∠B=∠C,
∴△BDF∽△CEF.
(2)∵∠BDF=90°,∠B=60°,
∴sin60°=
 =
=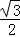 ,cos60°=
,cos60°=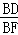 =
=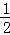 .
.∵BF=m,
∴DF=
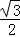 m,BD=
m,BD=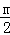 .
.∵AB=4,
∴AD=4﹣
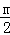 .
.∴S△ADF=
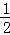 AD•DF
AD•DF=
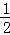 ×(4﹣
×(4﹣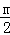 )×
)×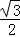 m
m=﹣
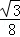 m2+
m2+ m.
m.同理:S△AEF=
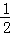 AE•EF
AE•EF=
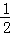 ×(4﹣
×(4﹣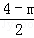 )×
)×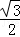 (4﹣m)
(4﹣m)=﹣
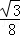 m2+2
m2+2 .
.∴S=S△ADF+S△AEF
=﹣
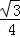 m2+
m2+ m+2
m+2
=﹣
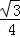 (m2﹣4m﹣8)
(m2﹣4m﹣8)=﹣
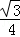 (m﹣2)2+3
(m﹣2)2+3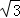 .其中0<m<4.
.其中0<m<4.∵﹣
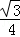 <0,0<2<4,
<0,0<2<4,∴当m=2时,S取最大值,最大值为3
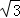 .
.∴S与m之间的函数关系为:
S═﹣
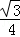 (m﹣2)2+3
(m﹣2)2+3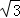 (其中0<m<4).
(其中0<m<4).当m=2时,S取到最大值,最大值为3
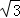 .
.(3)如图2,

∵A、D、F、E四点共圆,
∴∠EDF=∠EAF.
∵∠ADF=∠AEF=90°,
∴AF是此圆的直径.
∵tan∠EDF=
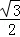 ,
,∴tan∠EAF=
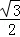 .
.∴
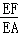 =
= .
.∵∠C=60°,
∴
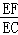 =tan60°=
=tan60°=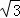 .
.设EC=x,则EF=
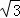 x,EA=2x.
x,EA=2x.∵AC=a,
∴2x+x=a.
∴x=
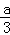 .
.∴EF=
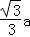 ,AE=
,AE=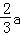 .
.∵∠AEF=90°,
∴AF=
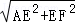 =
=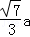 .
.∴此圆直径长为
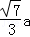 .
.
练习册系列答案
相关题目
 ,求⊙O的直径.
,求⊙O的直径.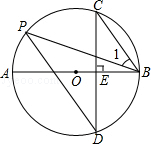



 的中点,OE交BC于点D.连接AC,若BC=6,DE=1,则AC的长为 .
的中点,OE交BC于点D.连接AC,若BC=6,DE=1,则AC的长为 .
