题目内容
已知一等腰三角形的底边长12,面积60,则这个等腰三角形的腰长是 .
分析:根据题意画出图形,过点A作AD⊥BC于点D,先根据三角形的面积求出AD的长,再根据勾股定理即可得出结论.
解答: 解:如图所示,△ABC中,AB=AC,BC=12,面积60,
解:如图所示,△ABC中,AB=AC,BC=12,面积60,
过点A作AD⊥BC于点D,
∵△ABC中,AB=AC,AD⊥BC,BC=12,
∴BD=
BC=6,
∵△ABC的面积等于60,
∴
BC•AD=60,即
×10AD=60,解得AFD=10,
∴AB=
=
=2
.
故答案为:2
.
 解:如图所示,△ABC中,AB=AC,BC=12,面积60,
解:如图所示,△ABC中,AB=AC,BC=12,面积60,过点A作AD⊥BC于点D,
∵△ABC中,AB=AC,AD⊥BC,BC=12,
∴BD=
| 1 |
| 2 |
∵△ABC的面积等于60,
∴
| 1 |
| 2 |
| 1 |
| 2 |
∴AB=
| AD2+BD2 |
| 102+62 |
| 34 |
故答案为:2
| 34 |
点评:本题考查的是勾股定理,熟知在任何一个直角三角形中,两条直角边长的平方之和一定等于斜边长的平方是解答此题的关键.

练习册系列答案
相关题目
 28、已知AB在平面直角坐标系中的位置如图所示,每个小正方形的边长为单位1.
28、已知AB在平面直角坐标系中的位置如图所示,每个小正方形的边长为单位1. 的周长等于24cm,且底边减去一腰长的差为3cm,那么这个三角形的底长为________cm.
的周长等于24cm,且底边减去一腰长的差为3cm,那么这个三角形的底长为________cm.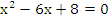 的两根,则这个三角形的周长为( )
的两根,则这个三角形的周长为( )