Question

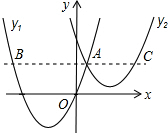如图，抛物线y1=a(x+2)2-3与y2=

1

2

(x-3)2+1交于点A（1，3），过点A作x轴的平行线，分别交两条抛物线于点B、C．则以下结论：
①无论x取何值，y₂的值总是正数；②a=

3

2

；③当x=0时，y₂-y₁=5；④当y₂＞y₁时，0≤x＜1；⑤2AB=3AC．
其中正确结论的编号是

①⑤

．

Answer 1

分析：①根据图象可以判断出图象都在x轴的上方，据此即可得知，无论x取何值，y₂的值总是正数；
②将点A（1，3）代入y1=a(x+2)2-3得a=

2

3

即可判断；
③将x=0分别代入y1=

2

3

(x+2)2-3和y2=

1

2

(x-3)2+1，求出y1与y2的值，再相减即可得到y₂-y₁的值；
④令y₂=y₁，求出两个函数的交点坐标，再根据图象判断x的取值范围；
⑤令

2

3

(x+2)2-3=3，

1

2

(x-3)2+1=3，分别解方程，求出A、B、C点的横坐标，再计算出AB、AC的长，即可做出正确判断．

解答：解：①由图可知，y₂的图象在x轴的上方，可见，无论x取何值，y₂的值总是正数，故本选项正确；
②将点A（1，3）代入抛物线y1=a(x+2)2-3，得a（1+2）²-3=3，解得a=

2

3

，故本选项错误；
③当x=0时，y₁=

2

3

(0+2)2-3=-

1

3

，y2=

1

2

(0-3)2+1=

11

2

，y₂-y₁=

11

2

+

1

3

=

35

6

，故本选项错误；
④令y₂=y₁，则有

2

3

(x+2)2-3=

1

2

(x-3)2+1，解得x₁=1，x₂=-35．几何图象可知，y₂＞y₁，-35＜x＜1，故本选项错误；
⑤令

2

3

(x+2)2-3=3，解得，x₁=1或x₂=-5；AB=5+1=6；

1

2

(x-3)2+1=3，解得，x₃=5，x₄=1；AB=5-1=4；
则2AB=3AC．故本选项正确．
故答案答案为①⑤．

点评：本题考查了二次函数的性质，数形结合是本题的核心，要善于利用图形进行解答．