题目内容
 如图,已知?ABCD,∠DAB与∠ABC的平分线交于点E.
如图,已知?ABCD,∠DAB与∠ABC的平分线交于点E.(1)∠AEB=
90
90
(度);(2)当?ABCD满足条件
CD=2AD
CD=2AD
时,点E刚好落在CD上.分析:(1)根据平行四边形的邻角互补求出∠DAB+∠ABC=180°,再根据角平分线的定义求出∠EAB+∠EBA=90°,然后根据三角形的内角和定理列式计算即可得解;
(2)根据角平分线的定义可得∠DAE=∠EAB,再根据两直线平行,内错角相等求出∠DEA=∠EAB,然后求出∠DAE=∠DEA,然后根据等角对等边的性质求出AD=DE,同理求出BC=CE,然后求解即可.
(2)根据角平分线的定义可得∠DAE=∠EAB,再根据两直线平行,内错角相等求出∠DEA=∠EAB,然后求出∠DAE=∠DEA,然后根据等角对等边的性质求出AD=DE,同理求出BC=CE,然后求解即可.
解答:解:(1)在?ABCD中,∠DAB+∠ABC=180°,
∵∠DAB与∠ABC的平分线交于点E,
∴∠EAB=
∠DAB,∠EBA=
∠ABC,
∴∠EAB+∠EBA=
(∠DAB+∠ABC)=
×180°=90°;
(2)∵∠DAB与∠ABC的平分线交于点E,
∴∠DAE=∠EAB,
∵点E落在CD上,
∴∠DEA=∠EAB,
∴∠DAE=∠DEA,
∴AD=DE,
同理可得BC=CE,
∴CD=DE+CE=AD+BC=2AD,
即CD=2AD.
故答案为:(1)90;(2)CD=2AD.
∵∠DAB与∠ABC的平分线交于点E,
∴∠EAB=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠EAB+∠EBA=
| 1 |
| 2 |
| 1 |
| 2 |
(2)∵∠DAB与∠ABC的平分线交于点E,

∴∠DAE=∠EAB,
∵点E落在CD上,
∴∠DEA=∠EAB,
∴∠DAE=∠DEA,
∴AD=DE,
同理可得BC=CE,
∴CD=DE+CE=AD+BC=2AD,
即CD=2AD.
故答案为:(1)90;(2)CD=2AD.
点评:本题考查了平行四边形的性质,主要利用了平行四边形的邻角互补,角平分线的定义,平行线的性质,以及等角对等边的性质,熟记各性质是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 14、如图,已知?ABCD中,AB=4,BC=6,BC边上的高AE=2,则DC边上的高AF的长是
14、如图,已知?ABCD中,AB=4,BC=6,BC边上的高AE=2,则DC边上的高AF的长是

 26、如图,已知?ABCD,AE平分∠BAD,交DC于E,DF⊥BC于F,交AE于G,且DF=AD.
26、如图,已知?ABCD,AE平分∠BAD,交DC于E,DF⊥BC于F,交AE于G,且DF=AD.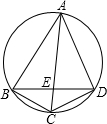 如图,已知ABCD是圆的内接四边形,对角线AC和BD相交于E,BC=CD=4,AE=6,如果线段BE和DE的长都是整数,则BD的长等于
如图,已知ABCD是圆的内接四边形,对角线AC和BD相交于E,BC=CD=4,AE=6,如果线段BE和DE的长都是整数,则BD的长等于 如图,已知ABCD是圆O的内接四边形,AB=BD,BM⊥AC于M,求证:AM=DC+CM.
如图,已知ABCD是圆O的内接四边形,AB=BD,BM⊥AC于M,求证:AM=DC+CM.