题目内容
 (2012•咸宁)如图,AB是⊙O的直径,点E是AB上的一点,CD是过E点的弦,过点B的切线交AC的延长线于点F,BF∥CD,连接BC.
(2012•咸宁)如图,AB是⊙O的直径,点E是AB上的一点,CD是过E点的弦,过点B的切线交AC的延长线于点F,BF∥CD,连接BC.(1)已知AB=18,BC=6,求弦CD的长;
(2)连接BD,如果四边形BDCF为平行四边形,则点E位于AB的什么位置?试说明理由.
分析:(1)由BF与⊙O相切,根据切线的性质,可得BF⊥AB,又由BF∥CD,易得CD⊥AB,由垂径定理即可求得CE=DE,然后连接CO,设OE=x,则BE=9-x,由勾股定理即可求得OE的长,继而求得CD的长;
(2)由四边形BDCF为平行四边形,根据平行四边形的性质,即可得CD=BF,又由△AEC∽△ABF,即可求得点E是AB的中点.
(2)由四边形BDCF为平行四边形,根据平行四边形的性质,即可得CD=BF,又由△AEC∽△ABF,即可求得点E是AB的中点.
解答: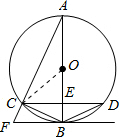 (1)解:∵BF与⊙O相切,
(1)解:∵BF与⊙O相切,
∴BF⊥AB.(1分)
而BF∥CD,
∴CD⊥AB.
又∵AB是直径,
∴CE=ED.(2分)
连接CO,设OE=x,则BE=9-x.
由勾股定理可知:CO2-OE2=BC2-BE2=CE2,
即92-x2=62-(9-x)2,
解得:x=7.(4分)
∴CD=2
=2
=8
.(5分)
(2)∵四边形BDCF为平行四边形,
∴BF=CD.
而CE=DE=
CD,
∴CE=
BF.(7分)
∵BF∥CD,
∴△AEC∽△ABF.(8分)
∴
=
=
.
∴点E是AB的中点.(9分)
 (1)解:∵BF与⊙O相切,
(1)解:∵BF与⊙O相切,∴BF⊥AB.(1分)
而BF∥CD,
∴CD⊥AB.
又∵AB是直径,
∴CE=ED.(2分)
连接CO,设OE=x,则BE=9-x.
由勾股定理可知:CO2-OE2=BC2-BE2=CE2,
即92-x2=62-(9-x)2,
解得:x=7.(4分)
∴CD=2
| CO2-OE2 |
| 92-72 |
| 2 |
(2)∵四边形BDCF为平行四边形,
∴BF=CD.
而CE=DE=
| 1 |
| 2 |
∴CE=
| 1 |
| 2 |
∵BF∥CD,
∴△AEC∽△ABF.(8分)
∴
| AE |
| AB |
| EC |
| BF |
| 1 |
| 2 |
∴点E是AB的中点.(9分)
点评:此题考查了切线的性质、相似三角形的判定与性质、垂径定理以及勾股定理等知识.此题难度适中,注意掌握数形结合思想与方程思想的应用.

练习册系列答案
相关题目
 (2012•咸宁)如图,在梯形ABCD中,AD∥BC,∠C=90°,BE平分∠ABC且交CD于E,E为CD的中点,EF∥BC交AB于F,EG∥AB交BC于G,当AD=2,BC=12时,四边形BGEF的周长为
(2012•咸宁)如图,在梯形ABCD中,AD∥BC,∠C=90°,BE平分∠ABC且交CD于E,E为CD的中点,EF∥BC交AB于F,EG∥AB交BC于G,当AD=2,BC=12时,四边形BGEF的周长为 转90°,得到线段AB.过点B作x轴的垂线,垂足为E,过点C作y轴的垂线,交直线BE于点D.运动时间为t秒.
转90°,得到线段AB.过点B作x轴的垂线,垂足为E,过点C作y轴的垂线,交直线BE于点D.运动时间为t秒. (2012•咸宁)如图,某公园入口处原有三级台阶,每级台阶高为18cm,深为30cm,为方便残疾人士,拟将台阶改为斜坡,设台阶的起点为A,斜坡的起始点为C,现设计斜坡BC的坡度i=1:5,则AC的长度是
(2012•咸宁)如图,某公园入口处原有三级台阶,每级台阶高为18cm,深为30cm,为方便残疾人士,拟将台阶改为斜坡,设台阶的起点为A,斜坡的起始点为C,现设计斜坡BC的坡度i=1:5,则AC的长度是 (2012•咸宁)如图,一次函数y1=kx+b的图象与反比例函数
(2012•咸宁)如图,一次函数y1=kx+b的图象与反比例函数