Question

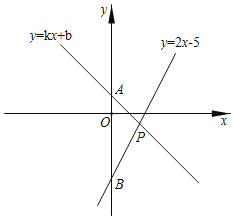
【题目】如图，在平面直角坐标系中，一次函数y＝kx+b的图象经过点A（0，1），且与直线y＝2x﹣5相交于点P，点P的横坐标为2，直线y＝2x﹣5与y轴交于点B．

（1）求k、b的值；

（2）求△ABP的面积；

（3）根据图象可得，关于x的不等式2x﹣5＞kx+b的解集是　 　；

（4）若点Q在x轴上，且满足S△ABQ＝S△ABP，则点Q的坐标是　 　．

Answer 1

【答案】（1）k=-1，b=1；（2）6；（3）x＞2；（4）（2，0）或（﹣2，0）．

【解析】

（1）利用待定系数法即可求k、b的值；

（2）求出点P的坐标即可求△ABP的面积；

（3）根据图象即可得关于x的不等式2x﹣5＞kx+b的解集；

（4）分两种情况确定点Q在x轴上，且满足S△ABQ＝S△ABP，即可求点Q的坐标．

解：（1）∵一次函数y＝kx+b的图象经过点A（0，1），

∴b＝1，

∵一次函数y＝kx+b的图象与直线y＝2x﹣5相交于点P，点P的横坐标为2，

∴点P的纵坐标为y＝2×2﹣5＝﹣1，

即P（2，﹣1），

把点P（2，﹣1）代入y＝kx+1中，得k＝﹣1，

答：k、b的值为﹣1、1；

（2）∵AB＝6，P（2，﹣1）．

∴S△ABP＝×6×2＝6．

答：△ABP的面积为6；

（3）∵一次函数y＝kx+b的图象与直线y＝2x﹣5相交于点P，点P的横坐标为2，

观察图象可知：

∴关于x的不等式2x﹣5＞kx+b的解集是x＞2；

故答案为x＞2．

（4）∵点Q在x轴上，且满足S△ABQ＝S△ABP，

∴S△ABQ＝×6×OQ＝6，

∴OQ＝2，

则点Q的坐标是（2，0）或（﹣2，0）．

故答案为：（2，0）或（﹣2，0）．