题目内容
函数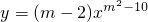
是反比例函数，并且图象在一、三象限，则m=________．
3
分析：根据反比例函数的定义可得m2-10=-1，根据函数图象分布在第一、三象限内，可得m-2＞0，然后求解即可．
解答：根据题意得，m2-10=-1且m-2＞0，
解得m1=3，m2=-3且m＞2，
所以m=3．
故答案为：3．
点评：本题考查了反比例函数的定义，反比例函数的性质，对于反比例函数y=
（k≠0），（1）k＞0，反比例函数图象在一、三象限；（2）k＜0，反比例函数图象在第二、四象限内．
分析：根据反比例函数的定义可得m2-10=-1，根据函数图象分布在第一、三象限内，可得m-2＞0，然后求解即可．
解答：根据题意得，m2-10=-1且m-2＞0，
解得m1=3，m2=-3且m＞2，
所以m=3．
故答案为：3．
点评：本题考查了反比例函数的定义，反比例函数的性质，对于反比例函数y=
（k≠0），（1）k＞0，反比例函数图象在一、三象限；（2）k＜0，反比例函数图象在第二、四象限内． 
练习册系列答案
名校课堂系列答案
相关题目
如图是反比例函数
市政府实施“万元增收工程”．农户小王自主创业，承包了部分土地种植果树．根据科学种植的经验，平均每棵甲种果树的产量y（千克）与种植棵数x（棵）之间满足关系y=-0.2x+40，平均每棵乙种果树的产量z（千克）与种植棵数x（棵）之间的部分对应值如下表：
（1）请观察题中的表格，用所学过的一次函数、反比例函数或二次函数的有关知识求出平均每棵乙种果树的产量z（千克）与种植棵数x（棵）之间的函数关系式；
（2）若小王种植甲、乙两种果树共200棵，其中种植甲种果树m棵，且甲种果树的种植数量不超过总数量的40%，试求果园的总产量w（千克）与甲种果树的种植数量w（棵）之间的函数关系式，并求出小王种植甲种果树多少棵时，果园的总产量最大，最大是多少？
（3）果园丰收，获得最大总产量．小王希望将两种水果均以6元/千克销售完．可按预计价格销 售时销量不佳，只售出了总产量的
．于是小王将售价降低a%，并迅速销售了总产量的
，这时，小王觉得这样销售下去不划算，于是又在降价后的价格基础上提价0.7a%把剩余水果卖完．最终一算，小王所得收益仅比原预期收益少2160元．请通过计算估计出整数a的值．
（参考数据：352=1225，362=1296，372=1369，382=1444）
| 种植棵数x（棵） | 60 | 65 | 80 | 92 |
| 平均每棵乙种果树的产量z（千克） | 32 | 30.5 | 26 | 22.4 |
（2）若小王种植甲、乙两种果树共200棵，其中种植甲种果树m棵，且甲种果树的种植数量不超过总数量的40%，试求果园的总产量w（千克）与甲种果树的种植数量w（棵）之间的函数关系式，并求出小王种植甲种果树多少棵时，果园的总产量最大，最大是多少？
（3）果园丰收，获得最大总产量．小王希望将两种水果均以6元/千克销售完．可按预计价格销 售时销量不佳，只售出了总产量的
| 1 |
| 6 |
| 1 |
| 3 |
（参考数据：352=1225，362=1296，372=1369，382=1444）
如图所示，在直角坐标系中，点A是反比例函数