题目内容
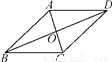
如图,菱形ABCD中,对角线AC,BD相交于点O,若再补充一个条件能使菱形ABCD成为正方形,则这个条件是____________.(补充一个即可)
练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案
相关题目
题目内容
如图,菱形ABCD中,对角线AC,BD相交于点O,若再补充一个条件能使菱形ABCD成为正方形,则这个条件是____________.(补充一个即可)

 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案