题目内容
如图,CE、CB是半圆O的切线,切点分别为D、B,AB为半圆O的直径.CE与BA的延长线交于点E,连接OC、OD.(1)求证:△OBC≌△ODC;
(2)若已知DE=a,AE=b,BC=c,请你思考后,从a,b,c三个已知数中
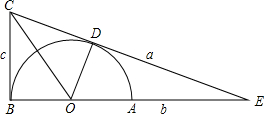 选用适当的数,设计出计算半圆O的半径r的一种方案:
选用适当的数,设计出计算半圆O的半径r的一种方案:①方案中你选用的已知数是
②写出求解过程(结果用字母表示).
分析:解:(1)CD、CB是半圆O的切线根据切线的性质知,∠0DC=∠0BC=90°,又由于半径OP=半径OB,公共边OC=OC,由HL判定△OBC≌△ODC;
(2)在Rt△ODE中,由勾股定理,得OD2+DE2=OE2即a2+r2=(b+r)2,a2=b2+2br.解得r=
,故可选用已知数为a、b.
(2)在Rt△ODE中,由勾股定理,得OD2+DE2=OE2即a2+r2=(b+r)2,a2=b2+2br.解得r=
| a2-b2 |
| 2b |
解答:(1)证明:CD、CB是半圆O的切线,
∴∠0DC=∠0BC=90°.
又∴0D=0B,OC=OC,
∴△OBC≌△ODC(HL).
(2)解:(此题答案不唯一)
①方案中选用的已知数是a、b;
②在Rt△ODE中,由勾股定理,得a2+r2=(b+r)2
∴a2=b2+2br.r=
;
①选用a、b、c,在Rt△BCE中用勾股定理得:r=
;
②选用a、b、c,由Rt△0DE∽Rt△cBE得,r=
;
③选用a、b、c,由连接AD,可证AD∥OC,得r=bc/a;
④若选a、c,可得r=
.
∴∠0DC=∠0BC=90°.
又∴0D=0B,OC=OC,
∴△OBC≌△ODC(HL).
(2)解:(此题答案不唯一)
①方案中选用的已知数是a、b;
②在Rt△ODE中,由勾股定理,得a2+r2=(b+r)2
∴a2=b2+2br.r=
| a2-b2 |
| 2b |
①选用a、b、c,在Rt△BCE中用勾股定理得:r=
| ||
| 2 |
②选用a、b、c,由Rt△0DE∽Rt△cBE得,r=
-b+
| ||
| 4 |
③选用a、b、c,由连接AD,可证AD∥OC,得r=bc/a;
④若选a、c,可得r=
c
| ||
| a+2c |
点评:本题利用了切线的性质,全等三角形的判定和性质,勾股定理求解,注意第(2)小题的答案不唯一.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
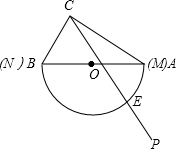 为O),现有射线CP绕点C从CA的位置开始按顺时针方向以每秒2度的速度旋转到CB位置,在旋转过程中,射线CP与量角器的半圆弧交于E.
为O),现有射线CP绕点C从CA的位置开始按顺时针方向以每秒2度的速度旋转到CB位置,在旋转过程中,射线CP与量角器的半圆弧交于E.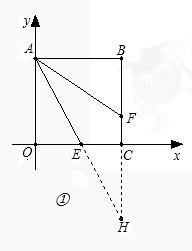 边上,且∠OAE=∠FAE
边上,且∠OAE=∠FAE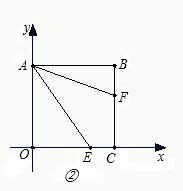
 (2012•武汉模拟)如图,AB为⊙O的直径,AM和BN是它的两条切线,E为⊙O的半圆弧上一动点(不与A、B重合),过点E的直线分别交射线AM、BN于D、C两点,且CB=CE.
(2012•武汉模拟)如图,AB为⊙O的直径,AM和BN是它的两条切线,E为⊙O的半圆弧上一动点(不与A、B重合),过点E的直线分别交射线AM、BN于D、C两点,且CB=CE. 我们新定义一种三角形:两边平方和等于第三边平方的2倍的三角形叫做奇异三角形.
我们新定义一种三角形:两边平方和等于第三边平方的2倍的三角形叫做奇异三角形. 到CB方向,在旋转过程中,射线CP与量角器的半圆弧交于E.
到CB方向,在旋转过程中,射线CP与量角器的半圆弧交于E.