题目内容
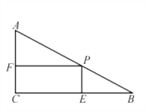
【题目】如图,在Rt△ABC中,∠C=90°,∠B=30°,AB=12cm,点P是AB边上的一个动点,过点P作PE⊥BC于点E,PF⊥AC于点F,当PB=6cm时,四边形PECF的面积最大,最大值为______
【答案】9![]() cm2
cm2
【解析】试题分析:设PE=x,在Rt△PEB中,根据∠B=30°,可知PB=2x,BE=![]() x,再在Rt△ABC中,利用三角函数的知识求出BC的长,进而可以表示出CE的长度;然后利用矩形的面积公式,即可得到四边形PECF的面积S关于x的表达式,对表达式进行配方,利用二次函数的最值即可得到答案.
x,再在Rt△ABC中,利用三角函数的知识求出BC的长,进而可以表示出CE的长度;然后利用矩形的面积公式,即可得到四边形PECF的面积S关于x的表达式,对表达式进行配方,利用二次函数的最值即可得到答案.
解:设PE=x,由∠B=30°,
得PB=2x,BE=![]() x.
x.
由AB=12cm,
得BC=12×cos30°=6![]() cm,
cm,
故CE=BC-BE=6![]() -
-![]() x.
x.
则四边形PECF的面积=CE×PE=(6![]() -
-![]() x)x=-
x)x=-![]() x2+6
x2+6![]() x=-
x=-![]() (x-3)2+9
(x-3)2+9![]() ,
,
当x=3cm,即PB=2x=6cm时,四边形PECF的面积最大,最大值是9![]() cm2.
cm2.
故答案为:9![]() cm2.
cm2.

练习册系列答案
相关题目