题目内容
如图所示,四边形ABCD是矩形,AD=16cm,AB=6cm。动点P、Q分别同时从A、C出发,点P以3cm/s的速度向D移动,直到D为止,Q以2cm/s的速度向B移动。
(1)P、Q两点从出发开始几秒后,四边形ABQP的面积是矩形面积的 ?何时四边形ABQP的面积最大,最大是多少?
?何时四边形ABQP的面积最大,最大是多少?
(2)P、Q从开始出发几秒后,PQ= cm?
cm?
(1)P、Q两点从出发开始几秒后,四边形ABQP的面积是矩形面积的
 ?何时四边形ABQP的面积最大,最大是多少?
?何时四边形ABQP的面积最大,最大是多少?(2)P、Q从开始出发几秒后,PQ=
 cm?
cm?
解:(1)矩形ABCD的面积S=16×6=96, S矩形=
S矩形= ×96=57.6,
×96=57.6,
可设x秒后,四边形ABQP的面积是矩形面积的 ,
,
即 (3x+16-2x)×6=
(3x+16-2x)×6= ×96,解得x=3.2秒,
×96,解得x=3.2秒,
由于点P的移动速度大于点Q的移动速度,
所以只有当点P移动到D点时,此时四边形ABQP的面积最大,
即3x=16,x= 秒,
秒,
S= (16+16-2×
(16+16-2× )×6=64平方厘米;
)×6=64平方厘米;
(2)可设出发y秒后PQ= cm,则由题意可得
cm,则由题意可得 ,解得y=0.8秒。
,解得y=0.8秒。
 S矩形=
S矩形= ×96=57.6,
×96=57.6,可设x秒后,四边形ABQP的面积是矩形面积的
 ,
,即
 (3x+16-2x)×6=
(3x+16-2x)×6= ×96,解得x=3.2秒,
×96,解得x=3.2秒,由于点P的移动速度大于点Q的移动速度,
所以只有当点P移动到D点时,此时四边形ABQP的面积最大,
即3x=16,x=
 秒,
秒,S=
 (16+16-2×
(16+16-2× )×6=64平方厘米;
)×6=64平方厘米;(2)可设出发y秒后PQ=
 cm,则由题意可得
cm,则由题意可得 ,解得y=0.8秒。
,解得y=0.8秒。
练习册系列答案
相关题目
 21、如图所示,四边形ABCD是平行四边形,E,F分别在AD,CB的延长线上,且DE=BF,连接FE分别交AB,CD于点H,G.
21、如图所示,四边形ABCD是平行四边形,E,F分别在AD,CB的延长线上,且DE=BF,连接FE分别交AB,CD于点H,G. 12、如图所示,四边形ABCD为⊙O的内接四边形,E为AB延长线的上一点,∠CBE=40°,则∠AOC等于( )
12、如图所示,四边形ABCD为⊙O的内接四边形,E为AB延长线的上一点,∠CBE=40°,则∠AOC等于( )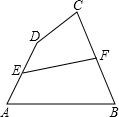 如图所示,四边形ABCD中,E、F分别为AD、BC的中点.
如图所示,四边形ABCD中,E、F分别为AD、BC的中点.
