题目内容
已知圆内接正六边形的边长为4cm,分别求出同圆中内接正三角形、正四边形的周长.
考点:正多边形和圆
专题:
分析:先根据圆内接正六边形的边长为4cm可知圆的半径为4cm,再画出图形,求出正三角形及正四边形的边长即可.
解答: 解:∵圆内接正六边形的边长为4cm,
解:∵圆内接正六边形的边长为4cm,
∴圆的半径为4cm.
如图1所示,
∵△ABC是等边三角形,
∴∠BOC=
=120°.
∵OD⊥BC,
∴∠BOD=60°,BC=2BD,
∵OB=4cm,
∴BD=OB•sin60°=4×
=2
cm,
∴BC=4
cm,
∴C△ABC=3×4
=12
cm;
如图2所示,
∵四边形ABCD是正方形,
∴∠OBD=45°,
∵OD⊥BC,
∴BD=OD,BC=2BD,
∵OB=4cm,
∴2BD2=16,解得BD=2
cm,
∴BC=4
cm,
∴C正方形ABCD=4×4
=16
cm.
 解:∵圆内接正六边形的边长为4cm,
解:∵圆内接正六边形的边长为4cm,∴圆的半径为4cm.
如图1所示,
∵△ABC是等边三角形,
∴∠BOC=
| 360° |
| 3 |
∵OD⊥BC,
∴∠BOD=60°,BC=2BD,
∵OB=4cm,
∴BD=OB•sin60°=4×
| ||
| 2 |
| 3 |
∴BC=4
| 3 |
∴C△ABC=3×4
| 3 |
| 3 |
如图2所示,
∵四边形ABCD是正方形,
∴∠OBD=45°,
∵OD⊥BC,
∴BD=OD,BC=2BD,
∵OB=4cm,
∴2BD2=16,解得BD=2
| 2 |
∴BC=4
| 2 |
∴C正方形ABCD=4×4
| 2 |
| 2 |
点评:本题考查的是正多边形和圆,根据题意画出图形,利用数形结合求解是解答此题的关键.

练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案
相关题目
 正方形ABCD中,E是CB延长线上一点,G是AE上一点,且AG=AD,AF⊥AE,交GD于F,GD交AB于H,求证:AF+BE=AE.
正方形ABCD中,E是CB延长线上一点,G是AE上一点,且AG=AD,AF⊥AE,交GD于F,GD交AB于H,求证:AF+BE=AE.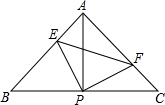 如图,已知△ABC中,AB=AC,∠BAC=90°,直角∠EPF的顶点P是BC中点,两边PE、PF分别交AB、AC于点E、F,给出以下四个结论:①AE=CF;②△EPF是等腰直角三角形;③S四边形AEPF=
如图,已知△ABC中,AB=AC,∠BAC=90°,直角∠EPF的顶点P是BC中点,两边PE、PF分别交AB、AC于点E、F,给出以下四个结论:①AE=CF;②△EPF是等腰直角三角形;③S四边形AEPF= 如图是一个长方体的展开图,每个面上都标注了字母,如果F面在前面,B面在左面,(字母朝外),那么在上面的字母是
如图是一个长方体的展开图,每个面上都标注了字母,如果F面在前面,B面在左面,(字母朝外),那么在上面的字母是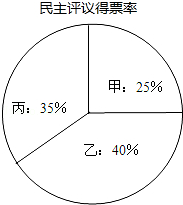 某单位欲从内部公开选拔一名管理人员,对甲、乙、丙三名候选人进行了笔试面试两项测试,三人的测试成绩如表:
某单位欲从内部公开选拔一名管理人员,对甲、乙、丙三名候选人进行了笔试面试两项测试,三人的测试成绩如表: