Question

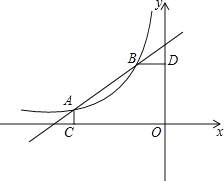
【题目】如图，在平面直角坐标系中，直线y=x+与反比例函数y=(x<0)的图象交于A(-4,a)、B(-1，b)两点，AC⊥x轴于C，BD⊥y轴于D．

（1）求a 、b及k的值；

（2）连接OA，OB，求△AOB的面积．

Answer 1

【答案】（1）a=，b=2，k= -2 ；（2）S△AOB =

【解析】

（1）把A、B两点坐标代入直线解析式求出a，b的值，从而确定A、B两点坐标，再把A（或B）点坐标代入双曲线解析式求出k的值即可；

（2）设直线AB分别交x轴、y轴于点E,F，根据S△AOB=S△EOF-S△AEO-S△BFO求解即可.

（1）将点A（-4，a）、B（-1，b）分别代入表达式中，得：

；，

∴A（-4，）、B（-1，2）

将B（-1,2）代入y=中，得k=-2

所以a=，b=2，k= -2

（2）设直线AB分别交x轴、y轴于点E,F，如图，

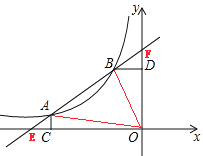
对于直线，分别令y=0，x=0，解得：

X=-5，y=，

∴E（-5,0），F（0，）

由图可知：

S△AEO=×OE×AC=，S△BFO=×OF×BD=，

S△EOF=×OE×OF=

∴S△AOB= S△EOF- S△AEO -S△BFO=