Question

现有点数为2，3，4的三张扑克牌，背面朝上洗匀，从中随机任意取出两张，点数分别为m和n（m≠n），则这样的有序数对（m，n）使关于x的方程mx-2=x+n的解不小于2的概率为________．

Answer 1

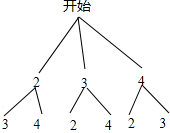
分析：先求出不等式的解为x=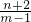，继而根据题意得出m、n的所有组合情况，分别代入即可得出符合题意的组合数，继而可得出概率．
解答：
总共的组合为：（2，3），（3，2），（2，4），（4，2），（3，4），（4，3）共6中，
mx-2=x+n的解为x=，
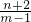要使方程的解不小于2，则x=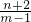≥2，
解得：2m-n≤4，
即可得满足题意的组合为：（2，3），（3，2），（2，4），（3，4），共4个．
故概率为：=．
故答案为：．
点评：此题考查了一元一次方程的解、列表法及树状图法的应用，解答本题的关键是利用树状图得出所有的m、n组合，然后代入检验．