题目内容
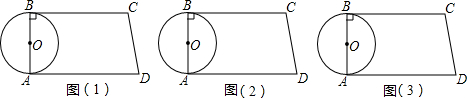
(2008•攀枝花)如图,在直角梯形ABCD中,AD∥BC,∠B=90°,AB为⊙O的直径,且AB=8cm,AD=16cm,BC=14cm,动点P从B点开始沿BC边向C点以1cm/s的速度运动,动点Q从点D开始沿DA边向A以3cm/s的速度运动;P、Q同时出发,当其中一点到达端点时,另一点也随之停止运动,设运动时间为t.
求:
(1)要使四边形PQDC为直角梯形和等腰梯形,t应分别为多少?
(2)要使直线PQ与⊙O相切,求t的值.
(3)分别写出当直线PQ与⊙O相交、相离时t的取值范围.(此问直接写出结果)

求:
(1)要使四边形PQDC为直角梯形和等腰梯形,t应分别为多少?
(2)要使直线PQ与⊙O相切,求t的值.
(3)分别写出当直线PQ与⊙O相交、相离时t的取值范围.(此问直接写出结果)
分析:(1)当BP=AQ时,四边形是直角梯形;根据AD-BC=2,可以得到:当DQ-PC=4时,四边形PQDC是等腰梯形,据此即可列方程求得t的值;
(2)过点P作PE⊥AD于E,则当PQ与⊙O相切时,根据切线长定理可得:PQ=BP+AQ,要使直线PQ与⊙O相切,则一定有(BP+AQ)2=AB2+QE2,据此即可列方程求得t的值;
(3)根据(2)解得的结果,t=
或t=4,直线PQ从开始运动时与圆相交,一直到当t=
时,直线与圆相切;再运动时,直线与圆相离,再到t=4时,直线与圆相切,然后相交,直到停止.
(2)过点P作PE⊥AD于E,则当PQ与⊙O相切时,根据切线长定理可得:PQ=BP+AQ,要使直线PQ与⊙O相切,则一定有(BP+AQ)2=AB2+QE2,据此即可列方程求得t的值;
(3)根据(2)解得的结果,t=
| 4 |
| 3 |
| 4 |
| 3 |
解答: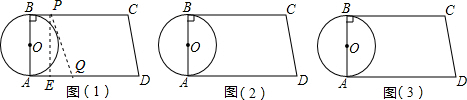 解:(1)由题意知:当t=16-3t,即t=4(秒)时,四边形PQDC是直角梯形;
解:(1)由题意知:当t=16-3t,即t=4(秒)时,四边形PQDC是直角梯形;
∵AD-BC=2,
∴当DQ-PC=4时,四边形PQDC是等腰梯形,
则3t-(14-t)=4,
解得:t=4.5(秒);
(2)过点P作PE⊥AD于E,则当PQ与⊙O相切时,有:
(BP+AQ)2=AB2+QE2
则(16-2t)2=82+(16-t-3t)2,
解得:t=
或t=4;
(3)直线PQ与⊙O相交时:0≤t<
或4<t≤
.
直线PQ与⊙O相离时:
<t<4.
 解:(1)由题意知:当t=16-3t,即t=4(秒)时,四边形PQDC是直角梯形;
解:(1)由题意知:当t=16-3t,即t=4(秒)时,四边形PQDC是直角梯形;∵AD-BC=2,
∴当DQ-PC=4时,四边形PQDC是等腰梯形,
则3t-(14-t)=4,
解得:t=4.5(秒);
(2)过点P作PE⊥AD于E,则当PQ与⊙O相切时,有:
(BP+AQ)2=AB2+QE2
则(16-2t)2=82+(16-t-3t)2,
解得:t=
| 4 |
| 3 |
(3)直线PQ与⊙O相交时:0≤t<
| 4 |
| 3 |
| 16 |
| 3 |
直线PQ与⊙O相离时:
| 4 |
| 3 |
点评:本题考查了直线与圆的位置关系,以及勾股定理,正确求得直线PQ与圆相切时t的值是关键.

练习册系列答案
相关题目
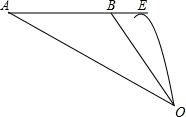 60°.飞机继续飞行0.1千米到达E处进行空投,已知空投物资在空中下落过程中的轨迹是抛物线,若要使空投物资刚好落在O处.
60°.飞机继续飞行0.1千米到达E处进行空投,已知空投物资在空中下落过程中的轨迹是抛物线,若要使空投物资刚好落在O处.