题目内容
如图，抛物线y=x2+bx+c经过A（-1，O），B（4，5）两点，请解答下列问题：（1）求抛物线的解析式；
（2）若抛物线的顶点为点D，对称轴所在的直线交x轴于点E，连接AD，点F为AD的中点，求出线段EF的长．
注：抛物线y=ax2+bx+c的对称轴是x=-
| b |
| 2a |
| b |
| 2a |
| 4ac-b2 |
| 4a |
分析：（1）将A（-1，O），B（4，5）两点代入y=x2+bx+c中，求b、c的值即可；
（2）根据抛物线解析式可求D、E三点坐标，根据中点坐标公式求F点坐标，再求线段EF的长度．
（2）根据抛物线解析式可求D、E三点坐标，根据中点坐标公式求F点坐标，再求线段EF的长度．
解答：
解：（1）把A（-1，O），B（4，5）两点代入y=x2+bx+c中，
得
，
解得
，
∴y=x2-2x-3；
（2）∵y=x2-2x-3=（x-1）2-4，
∴D（1，-4），E（1，0），
∵F点为A（-1，0）、D（1，-4）的中点，
∴F（0，-2），
∴EF=
=
．
解：（1）把A（-1，O），B（4，5）两点代入y=x2+bx+c中，得
|
解得
|
∴y=x2-2x-3；
（2）∵y=x2-2x-3=（x-1）2-4，
∴D（1，-4），E（1，0），
∵F点为A（-1，0）、D（1，-4）的中点，
∴F（0，-2），
∴EF=
| 12+22 |
| 5 |
点评：本题考查了二次函数的综合运用．关键是求出二次函数解析式，根据顶点坐标及对称轴解题．
练习册系列答案
相关题目
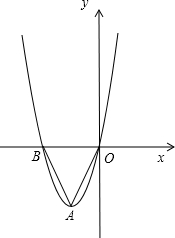如图，抛物线y=x2+4x与x轴分别相交于点B、O，它的顶点为A，连接AB，AO．
16、如图，抛物线y=-x2+2x+m（m＜0）与x轴相交于点A（x1，0）、B（x2，0），点A在点B的左侧．当x=x2-2时，y
已知如图，抛物线y=x2+（k2+1）x+k+1的对称轴是直线x=-1，且顶点在x轴上方．设M是直线x=-1左侧抛物线上的一动点，过点M作x轴的垂线MG，垂足为G，过点M作直线x=-1的垂线MN，垂足为N，直线x=-1与x轴的交于H点，若M点的横坐标为x，矩形MNHG的周长为l．
（2013•扬州）如图，抛物线y=x2-2x-8交y轴于点A，交x轴正半轴于点B．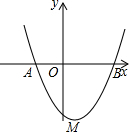
如图，抛物线y=x2-2x-3与x轴分别交于A，B两点．