Question

【题目】如图，在Rt中，，点为边上一个动点，过点作交边于，过点作射线交边于点，交射线于点，联结．设两点的距离为，两点的距离为．

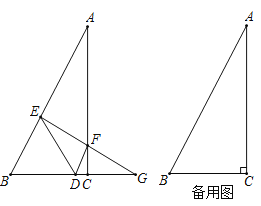
（1）求证：；

（2）求关于的函数解析式，并写出的取值范围；

（3）点在运动过程中，能否构成等腰三角形？如果能，请直接写出的长，如果不能，请简要说明理由．

Answer 1

【答案】（1）见解析；（2）y=2x-6（3≤x≤12）；（3）能，3或6-6或6

【解析】

（1）根据三角形的内角和定理先得∠B=60°，证明△BED是等边三角形，根据等角对等边分别证明DE=DG，BD=ED，可得结论；

（2）先得BC=6，根据直角三角形30度角的性质可得结论；

（3）分三种情况：①当ED=DF时，当F与C重合时，如图2，BE=BC=3；②当ED=EF时，如图3，根据直角三角形30度角的性质或三角函数列等式可得结论；③当EF=DF时，C与D重合，如图4，此时BE=BC=6；

（1）证明：如图1，

Rt△ABC中，∠A=30°，∠C=90°，

∴∠B=60°，

∵∠BDE=∠B=60°，

∴∠BED=60°，

∴△BED是等边三角形，

∴BD=ED，

∵EF⊥AB，

∴∠BEF=90°，

∴∠DEG=30°，

∵∠EDB=∠DEG+∠DGE，

∴∠DGE=60°-30°=30°=∠DEF，

∴DE=DG，

∴BD=DG；

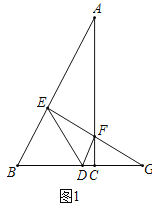
（2）解：如图1，Rt△ABC中，∠A=30°，∠C=90°，AB=12，

∴BC=6，

Rt△BEG中，∠G=30°，

∴BG=2BE，

∵BE两点的距离为x，CG两点的距离为y，

∴6+y=2x，y=2x-6（3≤x≤12）；

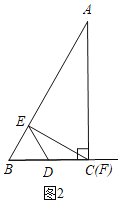
（3）解：分三种情况：

①当ED=DF时，当F与C重合时，如图2，BE=BC=3；

②当ED=EF时，如图3，

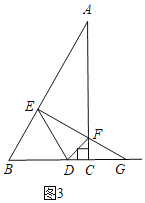
BE=ED=EF=x，

∴AE=12-x，

Rt△AEF中，tan∠A=，

∵∠A=30°，

∴，

∴x=6-6，

∴BE=6-6；

③当EF=DF时，C与D重合，如图4，此时BE=BC=6；

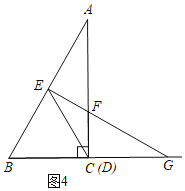
综上，当△DEF构成等腰三角形时，BE的长为3或6-6或6，