题目内容
如图，已知正五边形ABCDE的每一个角都相等．（1）求∠B；
（2）连AC，若∠BAC=∠BCA，求∠ACD．
分析：（1）首先求得多边形的内角和，即可求得每个内角的度数；
（2）利用等腰三角形的性质：等边对等角即可求解．
（2）利用等腰三角形的性质：等边对等角即可求解．
解答：解：（1）正五边形ABCDE的内角和是（5-2）×180=540°，
则∠B=
=108゜．
（2）在△ABC中，∵BA=BC，
∴∠BCA=
=36°．
∴∠ACD=∠BCD-∠BCA=108-36=72゜．
则∠B=
| 540 |
| 5 |
（2）在△ABC中，∵BA=BC，
∴∠BCA=
| 180°-∠B |
| 2 |
∴∠ACD=∠BCD-∠BCA=108-36=72゜．
点评：本题考查了多边形的内角和定理以及等腰三角形的性质定理，理解等腰三角形的性质定理是关键．
练习册系列答案
阅读快车系列答案
相关题目
如图，已知正五边形ABCDE的边长为4m．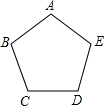
（2012•江西） 如图，已知正五边形ABCDE，请用无刻度的直尺，准确地画出它的一条对称轴（保留作图痕迹）．
如图，已知正五边形ABCDE的每一个角都相等．
如图，已知正五边形ABCDE中，BF与CM相交于点P，CF=DM．