题目内容
【题目】如图，已知⊙O的半径长为1，AB、AC是⊙O的两条弦，且AB=AC，BO的延长线交AC于点D，联结OA、OC．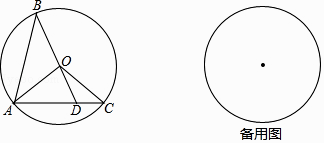
（1）求证：△OAD∽△ABD；
（2）当△OCD是直角三角形时，求B、C两点的距离；
（3）记△AOB、△AOD、△COD 的面积分别为S1、S2、S3 ， 如果S2是S1和S3的比例中项，求OD的长．
【答案】
（1）
证明：如图1中，
在△AOB和△AOC中，
，
∴△AOB≌△AOC，
∴∠C=∠B，
∵OA=OC，
∴∠OAC=∠C=∠B，∵∠ADO=∠ADB，
∴△OAD∽△ABD
（2）
解：如图2中，
∵BD⊥AC，OA=OC，
∴AD=DC，
∴BA=BC=AC，
∴△ABC是等边三角形，
在Rt△OAD中，∵OA=1，∠OAD=30°，
∴OD= 
OA= ，
∴AD= 
= 
，
∴BC=AC=2AD= 
（3）
解：如图3中，作OH⊥AC于H，设OD=x．
∵△DAO∽△DBA，
∴ 
= 
= 
，
∴ 
= 
= 
，
∴AD= 
，AB= 
，
∵S2是S1和S3的比例中项，
∴S22=S1S3，
∵S2= ADOH，S1=S△OAC= ACOH，S3= CDOH，
∴（ ADOH）2= ACOH 
CDOH，
∴AD2=ACCD，
∵AC=AB．CD=AC﹣AD= ﹣ ，
∴（ ）2= （ ﹣ ），
整理得x2+x﹣1=0，
解得x= 
或 
，
经检验：x= 是分式方程的根，且符合题意，
∴OD=
【解析】（1）由△AOB≌△AOC，推出∠C=∠B，由OA=OC，推出∠OAC=∠C=∠B，由∠ADO=∠ADB，即可证明△OAD∽△ABD；（2）如图2中，当△OCD是直角三角形时，可以证明△ABC是等边三角形即可解决问题；（3）如图3中，作OH⊥AC于H，设OD=x．想办法用x表示AD、AB、CD，再证明AD2=ACCD，列出方程即可解决问题；
