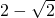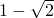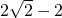题目内容
如图，数轴上A、B两点表示的实数分别是a、b，化简
=________．
-2a
分析：根据数轴表示数的方法得到a＜0＜b且|b|＞a，根据二次根式的性质得到原式=|a+b|-|a-b|，再根据绝对值的意义得到原式=-（a+b）-（a-b），然后去括号合并即可．
解答：∵b＜0＜a，且|b|＞a，
∴原式=|a+b|-|a-b|
=-（a+b）-（a-b）
=-a-b-a+b
=-2a．
故答案为-2a．
点评：本题考查了二次根式的性质：
=|a|．也考查了绝对值的意义和数轴．
分析：根据数轴表示数的方法得到a＜0＜b且|b|＞a，根据二次根式的性质得到原式=|a+b|-|a-b|，再根据绝对值的意义得到原式=-（a+b）-（a-b），然后去括号合并即可．
解答：∵b＜0＜a，且|b|＞a，
∴原式=|a+b|-|a-b|
=-（a+b）-（a-b）
=-a-b-a+b
=-2a．
故答案为-2a．
点评：本题考查了二次根式的性质：
=|a|．也考查了绝对值的意义和数轴． 
练习册系列答案
一卷搞定系列答案
名校作业本系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目
如图，数轴上两个点表示的数分别为a，b，则
如图，数轴上A、B两点所表示的两数的（ ）
两个实数对应的点分别为A、B，点C与点B关于点A对称（即AB=AC），则点C表示的数是
