题目内容
如图，圆O与正方形ABCD的两边AB、AD相切，且DE与圆O相切于E点．若圆O的半径为5，且AB=11，则DE的长度为何？
- A.5
- B.6
- C.
- D.
B
分析：求出正方形ANOM，求出AM长和AD长，根据DE=DM求出即可．
解答：
连接OM、ON，
∵四边形ABCD是正方形，
∴AD=AB=11，∠A=90°，
∵圆O与正方形ABCD的两边AB、AD相切，
∴∠OMA=∠ONA=90°=∠A，
∵OM=ON，
∴四边形ANOM是正方形，
∴AM=OM=5，
DE与圆O相切于E点，圆O的半径为5，
∴AM=5，DM=DE，
∴DE=11-5=6，
故选B．
点评：本题考查了正方形的性质和判定，切线的性质，切线长定理等知识点的应用，关键是求出AM长和得出DE=DM．
分析：求出正方形ANOM，求出AM长和AD长，根据DE=DM求出即可．
解答：
连接OM、ON，
∵四边形ABCD是正方形，
∴AD=AB=11，∠A=90°，
∵圆O与正方形ABCD的两边AB、AD相切，
∴∠OMA=∠ONA=90°=∠A，
∵OM=ON，
∴四边形ANOM是正方形，
∴AM=OM=5，
DE与圆O相切于E点，圆O的半径为5，
∴AM=5，DM=DE，
∴DE=11-5=6，
故选B．
点评：本题考查了正方形的性质和判定，切线的性质，切线长定理等知识点的应用，关键是求出AM长和得出DE=DM．
练习册系列答案
名校课堂系列答案
相关题目
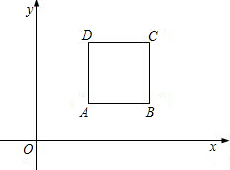如图，四边形ABCD是正方形，已知A（5，4），B（10，4）：
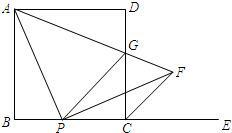一点，连接AP．过点P作PF⊥AP，与∠DCE的平分线CF相交于点F．连接AF，与边CD相交于点G，连接PG．
（2013•台湾）如图，圆O与正方形ABCD的两边AB、AD相切，且DE与圆O相切于E点．若圆O的半径为5，且AB=11，则DE的长度为何？（ ）
