题目内容
如图,在菱形ABCD中,对角线AC、BD相交于点O,且AC=12,BD=16,E为AD的中点,点P在BD上移动,若△POE为等腰三角形,则所有符合条件的点P共有 个.

考点:
菱形的性质;等腰三角形的性质.
专题:
证明题.
分析:
首先可以确定的P点有3个:①以O为圆心OE为半径作圆,与BD交于两点,都符合P点的要求;②连接OE,OE的中垂线交BD于一点,此点也符合P点要求;
然后连接OE,过E作OD的垂线EF,易得EF是△AOD的中位线,结合菱形的性质可证得EF垂直平分OD,因此OE=DE,即D点也符合P点的要求,所以共有4个点P.
解答:
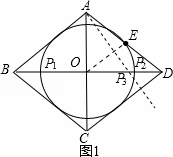
解:如图①,首先可以确定的P点有三个:
一、以O为圆心OE为半径作圆,⊙O交BD于P1、P2;
二、连接OE,作OE的垂直平分线,交BD于P3;
如图②,连接OE,过E作EF⊥OD于F;
由于四边形ABCD是菱形,故AO⊥OD,即EF∥AO;
又∵E是AD中点,
∴F是OD的中点,
∴EF是△AOD的中位线,
即EF垂直平分OD,
∴OE=DE,故D点符合P点的要求;
综上所述,符合条件的P点有4个.

故答案为4.
点评:
此题主要考查了菱形的性质以及等腰三角形的判定,由于等腰三角形的腰和底不确定,一定要分类讨论,以免漏解.

练习册系列答案
相关题目
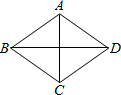 如图:在菱形ABCD中,AC=6,BD=8,则菱形的边长为( )
如图:在菱形ABCD中,AC=6,BD=8,则菱形的边长为( )| A、5 | B、10 | C、6 | D、8 |
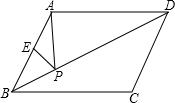
 ME交射线CD于点N,连接MD、AN.
ME交射线CD于点N,连接MD、AN. (2013•攀枝花)如图,在菱形ABCD中,DE⊥AB于点E,cosA=
(2013•攀枝花)如图,在菱形ABCD中,DE⊥AB于点E,cosA= 如图,在菱形ABCD中,AE⊥BC,垂足为F,EC=1,∠B=30°,求菱形ABCD的周长.
如图,在菱形ABCD中,AE⊥BC,垂足为F,EC=1,∠B=30°,求菱形ABCD的周长.