��Ŀ����
����Ŀ���Ķ����в��ϣ���ɣ�1������2��С��.��ƽ��ֱ������ϵ�У���֪![]() ��������
��������![]() ��
��![]() �ľ������
�ľ������![]() �����
�����![]() ��
��![]() ��ƽ�����������㣬���ǿ���ͨ������ֱ������������
��ƽ�����������㣬���ǿ���ͨ������ֱ������������![]() ��ľ��룬��ͼ1������
��ľ��룬��ͼ1������![]() ��
��![]() �ֱ���
�ֱ���![]() �ᡢ
�ᡢ![]() ��������
��������![]() ��
��![]() ��
��![]() ��
��![]() ������ֱ���
������ֱ���![]() ��
��![]() ��
��![]() ��
��![]() ��ֱ��
��ֱ��![]() ��
��![]() �ڵ�
�ڵ�![]() ����
����![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ,���dzƴ˹�ʽ
,���dzƴ˹�ʽ![]() Ϊƽ��ֱ������ϵ����������
Ϊƽ��ֱ������ϵ����������![]() ��
��![]() ��ľ��빫ʽ
��ľ��빫ʽ
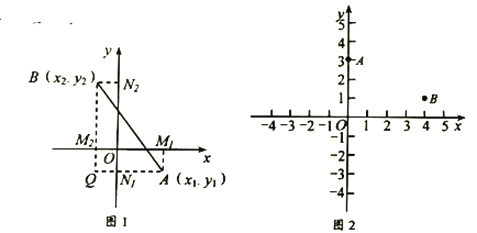
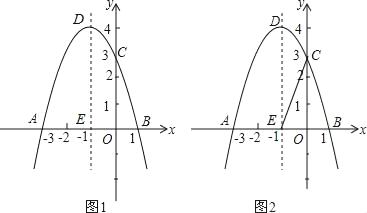
��1��ֱ��Ӧ��ƽ�����������빫ʽ�����![]() ��
��![]() �ľ���Ϊ_________
�ľ���Ϊ_________
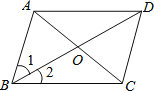
��2����ͼ2����֪��ƽ��ֱ������ϵ��������![]() ��
��![]() ��
��![]() Ϊ
Ϊ![]() ��������һ�㣬��
��������һ�㣬��![]() ����Сֵ
����Сֵ
���𰸡���1��5����2��![]()
��������
��1�����������ľ��빫ʽ![]() ���
���
��2������![]() ����
����![]() ��ԳƵĵ�
��ԳƵĵ�![]() ������
������![]() ����
����![]() ����
����![]() ��
��![]() �㼴Ϊ���������������ľ��빫ʽ��⼴�ɡ�
�㼴Ϊ���������������ľ��빫ʽ��⼴�ɡ�
�⣺��1��![]()
�ʴ�Ϊ��5
��2����ͼ2������![]() ����
����![]() ��ԳƵĵ�
��ԳƵĵ�![]() ������
������![]() ����
����![]() ����
����![]() ��
��![]() �㼴Ϊ����
�㼴Ϊ����

��![]() ��
��![]()
��![]()
��![]() ����СֵΪ
����СֵΪ![]()

��ϰ��ϵ�д�
 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
�����Ŀ