题目内容
【题目】问题提出
旋转是图形的一种变换方式，利用旋转来解决几何问题往往可以使解题过程更简单，起到事半功倍的效果．
初步思考
（
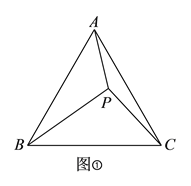
）如图①，点
是等边
内部一点，且
， 
， 
．求
的长．
小敏在解答此题时，利用了“旋转法”进行证明，她的方法如下：
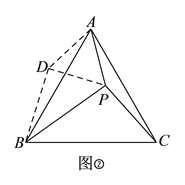
如图②，将
绕点
按顺时针方向旋转
后得到
，连接
．（请你在下面的空白处完成小敏的证明过程．）
推广运用
（
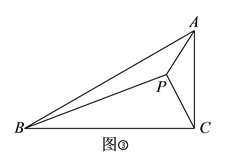
）如图③，在
中， 
， 
，点 
是
内部一点，且
， 
， 
．求
的长．
【答案】（1）
；（2）
【解析】试题分析：（1）只要证明△ADP是等边三角形，△PDB是直角三角形，两个勾股定理即可解决问题；（2）如图，作∠CAD=∠BAP，使AD=
AP．连接CD、PD．只要证明△DPC是直角三角形，即可解决问题；
试题解析：（
）∵将
绕点
按顺时针方向旋转
得到
，
∴
， 
， 
， 
．
∵
， 
，
∴
为等边三角形 ．
∴
， 
．
又
，
∴
．
在
中， 
， 
，
∴
．
（2）如图，作
，使
．连接
、
，
∵
， 
，
∴
，
又
，
∴
，
∴
，
在
中， 
， 
， 
，
易证
， 
．
∴
．
在
中，由勾股定理可得， 
．
练习册系列答案
考前必练系列答案
相关题目
