题目内容
如图,正方形ABCD的边长为1,点E是AD边上的动点,从点A沿AD向D运动,以BE为边,在BE的上方作正方形BEFG,连接CG.请探究:

(1)线段AE与CG是否相等?请说明理由.
(2)若设 ,
, ,当
,当 取何值时,
取何值时, 最大?
最大?
(3)连接BH,当点E运动到AD的何位置时,△BEH∽△BAE?
(1) 理由见解析;
理由见解析;
(2)当 时,
时, 有最大值为
有最大值为 ;
;
(3)当E点是AD的中点时,△BEH∽△BAE
【解析】
试题分析:(1)AE=CG,要证结论,必证△ABE≌△CBG,由正方形的性质很快确定∠3=∠4,又AB=BC,BE=BG,符合SAS即证.
(2)先证△ABE∽△DEH,所以 ,即可求出函数解析式y=-x2+x,继而求出最值.
,即可求出函数解析式y=-x2+x,继而求出最值.
(3)要使△BEH∽△BAE,需 ,又因为△ABE∽△DEH,所以
,又因为△ABE∽△DEH,所以 ,即
,即 ,所以当E点是AD的中点时,△BEH∽△BAE.
,所以当E点是AD的中点时,△BEH∽△BAE.
试题解析:(1) 理由:
理由:
正方形ABCD和正方形BEFG中



∴ 
又
∴△ABE≌△CBG
∴  ;
;
(2)∵正方形ABCD和正方形BEFG
∴
∴ 

∴ 
又∵
∴△ABE∽△DEH
∴
∴ 
∴ 

当 时,
时, 有最大值为
有最大值为 ;
;
(3)当E点是AD的中点时,△BEH∽△BAE
理由:∵ E是AD中点
∴ 
∴ 
又∵△ABE∽△DEH
∴ 
又∵ 
∴ 
又
∴ △BEH∽△BAE
考点:1.二次函数的综合应用2.正方形的性质3.相似三角形的判定

练习册系列答案
相关题目
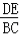 的值为 .
的值为 .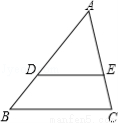
 (B)
(B) (C)
(C) (D)
(D)
 放置在平面直角坐标系中,顶点
放置在平面直角坐标系中,顶点 与坐标原点
与坐标原点 重合,点
重合,点 在
在 轴上.将正方形
轴上.将正方形 第一次落在
第一次落在 点的坐标是________,
点的坐标是________,
 ,
, ,
, ,
, ,则
,则 的值等于( ).
的值等于( ).
 B.
B.  C.
C. D.
D. 
 ;
;