题目内容
4.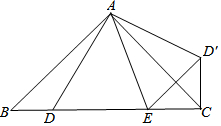 如图,已知△ABC中,∠BAC=90°,AB=AC,D、E是BC边上的点,将△ABD绕点A旋转,得到△ACD′.
如图,已知△ABC中,∠BAC=90°,AB=AC,D、E是BC边上的点,将△ABD绕点A旋转,得到△ACD′.(1)当∠DAE=45°时,求证:DE=D′E;
(2)在(1)得条件下,猜想:BD2、DE2、CE2有怎样的数量关系?请写出,并说明理由.
分析 (1)利用旋转的性质得AD=AD′,∠DAD′=∠BAC=90°,再计算出∠EAD′=∠DAE=45°,则利用“SAS”可判断△AED≌△AED′,所以DE=D′E;
(2)由(1)知△AED≌△AED′得到ED=ED′,∠B=∠ACD′,再根据等腰直角三角形的性质得∠B=∠ACB=45°,则根据性质得性质得BD=CD′,∠B=∠ACD′=45°,所以∠BCD′=∠ACB+∠ACD′=90°,于是根据勾股定理得CE2+D′C2=D′E2,所以BD2+CE==DE2.
解答 (1)证明:∵△ABD绕点A旋转,得到△ACD′,
∴AD=AD′,∠DAD′=∠BAC=90°,
∵∠DAE=45°
∴∠EAD′=∠DAD′-∠DAE=90°-45°=45°,
∴∠EAD′=∠DAE,
在△AED与△AED′中
$\left\{\begin{array}{l}{AE=AE}\\{∠EAD=∠EAD′}\\{AD=AD′}\end{array}\right.$,
∴△AED≌△AED′,
∴DE=D′E;
(2)解:BD2+CE==DE2.理由如下:
由(1)知△AED≌△AED′得到:ED=ED′,∠B=∠ACD′,
在△ABC中,AB=AC,∠BAC=90°,
∴∠B=∠ACB=45°,
∵△ABD绕点A旋转,得到△ACD′
∴BD=CD′,∠B=∠ACD′=45°,
∴∠BCD′=∠ACB+∠ACD′=45°+45°=90°,
在Rt△CD′E中,CE2+D′C2=D′E2,
∴BD2+CE==DE2.
点评 本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.也考查了等腰直角三角形的性质.

练习册系列答案
相关题目
12.某食堂购进30袋大米,每袋以50千克为标准,超过的记为正,不足的记为负,称重记录如表.
(1)这30袋大米的总重量比标准总重量是多还是少?相差多少?
(2)大米单价是每千克5.5元,食堂购进大米总共花多少钱?
| 与标准重量偏差(单位:千克) | -2 | -1 | 0 | 1 | 2 | 3 |
| 袋 数 | 5 | 10 | 3 | 1 | 5 | 6 |
(2)大米单价是每千克5.5元,食堂购进大米总共花多少钱?
9.下列二次根式中,与$\sqrt{2}$是同类二次根式的是( )
| A. | $\sqrt{0.2}$ | B. | $\sqrt{6}$ | C. | $\sqrt{8}$ | D. | $\sqrt{20}$ |
14.下列条件中,能判定△ABC≌△DEF的是( )
| A. | AB=DE,BC=EF,∠A=∠D | B. | ∠A=∠D,∠C=∠F,∠B=∠E | ||
| C. | ∠B=∠E,∠A=∠D,AC=EF | D. | ∠B=∠E,∠A=∠D,AB=DE |
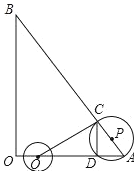 如图,在△AOB中,∠AOB为直角,OA=6,OB=8,半径为2的动圆圆心Q从点O出发,沿着OA方向以1个单位长度/秒的速度匀速运动,同时动点P从点A出发,沿着AB方向也以1个单位长度/秒的速度匀速运动,设运动时间为t秒(0<t≤5)以P为圆心,PA长为半径的⊙P与AB、OA的另一个交点分别为C、D,连结CD、QC.
如图,在△AOB中,∠AOB为直角,OA=6,OB=8,半径为2的动圆圆心Q从点O出发,沿着OA方向以1个单位长度/秒的速度匀速运动,同时动点P从点A出发,沿着AB方向也以1个单位长度/秒的速度匀速运动,设运动时间为t秒(0<t≤5)以P为圆心,PA长为半径的⊙P与AB、OA的另一个交点分别为C、D,连结CD、QC.