题目内容
不透明的口袋里装有红、黄、蓝三种颜色的小球(除颜色不同外,其它都一样),其中红球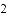
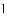
 .
.
(1)求袋中黄球的个数;
(2)第一次摸出一个球(不放回),第二次再摸出一个球,请用树状图或列表法求两次摸出的都是红球的概率.
练习册系列答案
相关题目
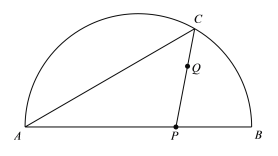
如图,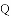
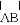 与弦
与弦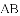
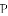
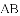
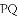
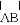 于点
于点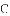
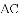
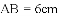
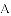
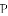
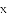
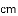
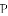
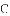
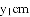 ,
,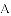
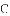
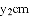 .
.
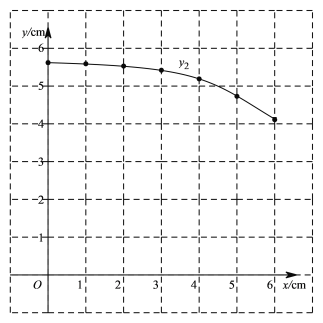
小腾根据学习函数的经验,分别对函数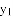 ,
,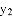 随自变量
随自变量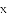
下面是小腾的探究过程,请补充完整:
(1)按照下表中自变量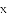
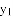 ,
,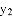 与
与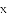
| 0 | 1 | 2 | 3 | 4 | 5 | 6 |
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
(2)在同一平面直角坐标系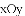
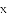
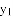 ),(
),(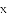
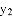 ),并画出函数
),并画出函数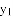 ,
,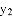 的图象;
的图象;
(3)结合函数图象,解决问题:当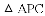
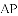
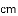


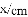
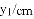
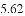
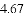
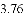
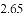
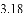
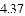
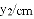
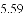
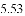
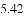
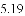
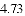
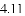
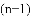
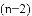
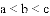
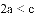
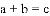
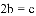
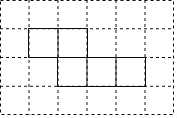
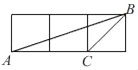
 B.
B. 
 D.
D. 
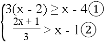 .
.