题目内容
 如图,O为直线AB上一点,OC平分∠AOE,∠DOE=90°,则以下结论正确的是( )
如图,O为直线AB上一点,OC平分∠AOE,∠DOE=90°,则以下结论正确的是( )①∠AOD与∠BOE互为余角; ②∠AOD=
| 1 |
| 2 |
③∠BOE=2∠COD;④若∠BOE=57°50′,则∠COE=61°5′.
| A、①④ | B、①③④ |
| C、③④ | D、①②③④ |
分析:由平角的定义与∠DOE=90°,即可求得∠AOD与∠BOE互为余角;又由角平分线的定义,可得∠AOC=2∠COE=2∠AOC,即可求得若∠BOE=57°50′,则∠COE=61°5′.
解答:解:∵∠DOE=90°,
∴∠COD+∠COE=90°,∠EOB+∠DOA=90°,(①正确)
∵OC平分∠AOE,
∴∠AOC=2∠COE=2∠AOC,
④若∠BOE=57°50′,
∵∠AOE+∠BOE=180°,
∴∠COE=
(180°-∠BOE)=61°5′.
∴①④正确.
故选A.
∴∠COD+∠COE=90°,∠EOB+∠DOA=90°,(①正确)
∵OC平分∠AOE,
∴∠AOC=2∠COE=2∠AOC,
④若∠BOE=57°50′,
∵∠AOE+∠BOE=180°,
∴∠COE=
| 1 |
| 2 |
∴①④正确.
故选A.
点评:此题考查了平角的定义与角平分线的定义.题目很简单,解题时要仔细识图.

练习册系列答案
相关题目
 17、如图,O为直线AB上一点,∠COB=26°30′,则∠1=
17、如图,O为直线AB上一点,∠COB=26°30′,则∠1=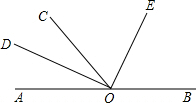 如图,O为直线AB上一点,∠AOC=50°,OD平分∠AOC,∠DOE=90°.
如图,O为直线AB上一点,∠AOC=50°,OD平分∠AOC,∠DOE=90°.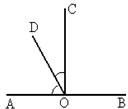 13、如图,O为直线AB上一点,OC平分∠AOB,∠COD=34°20′,则∠AOD=
13、如图,O为直线AB上一点,OC平分∠AOB,∠COD=34°20′,则∠AOD= 如图,O为直线AB上一点,∠AOC=50°,OD平分∠AOC,∠DOE=90°
如图,O为直线AB上一点,∠AOC=50°,OD平分∠AOC,∠DOE=90° 如图,O为直线AB上一点,OC平分∠AOD,3∠AOC=∠BOC,
如图,O为直线AB上一点,OC平分∠AOD,3∠AOC=∠BOC,