题目内容
若m<
,则关于x的一元二次方程(m-2)2x2+(2m+1)x+1=0根的情况是 .
| 3 |
| 4 |
考点:根的判别式
专题:
分析:先求出△的值,再根据△>0?方程有两个不相等的实数根;△=0?方程有两个相等的实数;△<0?方程没有实数根,进行判断即可.
解答:解:∵△=(2m+1)2-4×(m-2)2×1=20m-15,
又∵m<
,
∴20m-15<0,即△<0,
∴关于x的一元二次方程(m-2)2x2+(2m+1)x+1=0无实数根;
故答案为:无实数根.
又∵m<
| 3 |
| 4 |
∴20m-15<0,即△<0,
∴关于x的一元二次方程(m-2)2x2+(2m+1)x+1=0无实数根;
故答案为:无实数根.
点评:此题考查了根的判别式,一元二次方程根的情况与判别式△的关系:(1)△>0?方程有两个不相等的实数根;(2)△=0?方程有两个相等的实数;(3)△<0?方程没有实数根.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
下列各式:
(1-x),
,
,
,其中分式共有( )
| 1 |
| 3 |
| 4x |
| π-3 |
| x2-y2 |
| 2 |
| 5x2 |
| x |
| A、1个 | B、2个 | C、3个 | D、4个 |
计算:-3(1-
x),正确的是( )
| 1 |
| 6 |
A、-3-
| ||
| B、-3+2x | ||
C、-3+
| ||
D、-3-
|
下面的图案中,不是轴对称图形的是( )
A、 |
B、 |
C、 |
D、 |
一元二次方程x(x-2)=0的根是( )
| A、0 | B、2 | C、0和2 | D、无解 |
下列约分正确的是( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
 著名画家达芬奇不仅画意超群,同时还是一个数学家,发明家.他增进设计过一种圆规.如图所示,有两个互相垂直的话槽(滑槽宽度忽略不计)一根没有弹性的木棒的两端A,B能在滑槽内自由滑动,将笔插入位于木棒中点P处的小孔中,随着木棒的滑动就可以画出一个圆来,若AB=10cm,则画出的圆半径为
著名画家达芬奇不仅画意超群,同时还是一个数学家,发明家.他增进设计过一种圆规.如图所示,有两个互相垂直的话槽(滑槽宽度忽略不计)一根没有弹性的木棒的两端A,B能在滑槽内自由滑动,将笔插入位于木棒中点P处的小孔中,随着木棒的滑动就可以画出一个圆来,若AB=10cm,则画出的圆半径为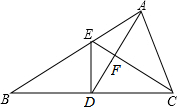 如图,已知△ABC中,D为BC中点,AD=AC,DE⊥BC,DE与AB交于E,EC与AD相交于点F,
如图,已知△ABC中,D为BC中点,AD=AC,DE⊥BC,DE与AB交于E,EC与AD相交于点F,