题目内容

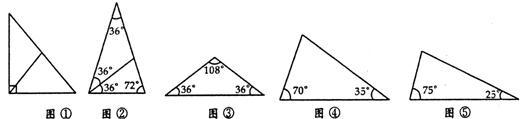
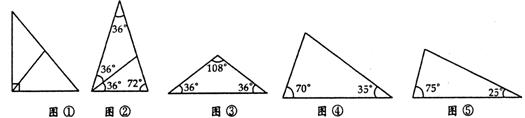
△ABC中，有一内角为36°，过顶点A的直线AD将△ABC分成2个等腰三角形，则满足上述条件的不同形状（相似的认为是同一形状）的△ABC最多有

个．

分析：利用36°的角是底角，可以作出角分别为36°、36°+54°，54°和36°、18°、126°的三角形，将36°的角分为24°和
12°，构造等腰三角形，再进行拼接，又可构成三角为36°、12°、132°的三角形．

解答：解：如图所示：

综上：共有5种满足上述的不同形状的三角形．
故答案是：5．

点评：本题考查了三角形的边角关系．培养学生的空间想象能力，重视知识的发生过程，让学生体验学习的过程．

练习册系列答案

全能闯关冲刺卷系列答案

1.试试看，你能把图③、图④、图⑤中的三角形分成两个等腰三角形吗

2.△ABC中，有一内角为36°，过某一顶点的直线将△ABC分成两个等腰三角形，则满足上述条件的不同形状（相似的认为是同一形状）的△ABC最多有5种，除了图②、图③中的两种，还有三种，请你画出来

我们知道：直角三角形斜边上的中线等于斜边的一半，说明斜边上的中线可把直角三角形分成两个等腰三角形（图①）．又比如，顶角为36°的等腰三角形也能分成两个等腰三角形（图②）．
（1）试试看，你能把图③、图④、图⑤中的三角形分成两个等腰三角形吗？
（2）△ABC中，有一内角为36°，过某一顶点的直线将△ABC分成两个等腰三角形，则满足上述条件的不同形状（相似的认为是同一形状）的△ABC最多有5种，除了图②、图③中的两种，还有三种，请你画出来．

试题分类