题目内容
如图,已知AB⊥MN,垂足为点B,P是射线BN上的一个动点,AC⊥AP,∠ACP=∠BAP,AB=4,BP=x,CP=y,点C到MN的距离为线段CD的长.
(1)求y关于x的函数解析式,并写出自变量x的取值范围.
(2)在点P的运动过程中,点C到MN的距离是否会发生变化?如果发生变化,请用x的代数式表示这段距离;如果不发生变化,请求出这段距离.

(1)求y关于x的函数解析式,并写出自变量x的取值范围.
(2)在点P的运动过程中,点C到MN的距离是否会发生变化?如果发生变化,请用x的代数式表示这段距离;如果不发生变化,请求出这段距离.

分析:(1)求y关于x的函数解析式,可以证明△ABP∽△CAP,根据相似比得出;
(2)C到MN的距离,即CD的长,可以延长CA交直线MN于点E,证得△EPC为等腰三角形,于是点A是EC的中点,则AB为△ECD的中位线,由三角形中位线定理求得CD=2AB=8.
(2)C到MN的距离,即CD的长,可以延长CA交直线MN于点E,证得△EPC为等腰三角形,于是点A是EC的中点,则AB为△ECD的中位线,由三角形中位线定理求得CD=2AB=8.
解答: 解:(1)∵AB⊥MN,AC⊥AP,
解:(1)∵AB⊥MN,AC⊥AP,
∴∠ABP=∠CAP=90°.
又∵∠ACP=∠BAP,
∴△ABP∽△CAP.
∴
=
.
即
=
,
∴所求的函数解析式为y=x+
(x>0);
(2)CD的长不会发生变化.
解法一:如图1,延长CA交直线MN于点E.
∵AC⊥AP,
∴∠PAE=∠PAC=90°.
∵∠ACP=∠BAP,
∴∠APC=∠APE.
∴∠AEP=∠ACP.
∴PE=PC.
∴AE=AC.
∵AB⊥MN,CD⊥MN,
∴AB∥CD.
∴AB是△ECD的中位线,
∵AB=4,
∴CD=2AB=8.
解法二:如备用图,过点C作CE⊥BA延长线于点E,AF⊥PC于点F.证出AE=AF=AB,于是CD=2AB=8.
 解:(1)∵AB⊥MN,AC⊥AP,
解:(1)∵AB⊥MN,AC⊥AP,∴∠ABP=∠CAP=90°.
又∵∠ACP=∠BAP,
∴△ABP∽△CAP.
∴
| BP |
| AP |
| AP |
| CP |
即
| x | ||
|
| ||
| y |
∴所求的函数解析式为y=x+
| 16 |
| x |
(2)CD的长不会发生变化.
解法一:如图1,延长CA交直线MN于点E.
∵AC⊥AP,
∴∠PAE=∠PAC=90°.
∵∠ACP=∠BAP,
∴∠APC=∠APE.
∴∠AEP=∠ACP.
∴PE=PC.
∴AE=AC.
∵AB⊥MN,CD⊥MN,
∴AB∥CD.
∴AB是△ECD的中位线,
∵AB=4,
∴CD=2AB=8.
解法二:如备用图,过点C作CE⊥BA延长线于点E,AF⊥PC于点F.证出AE=AF=AB,于是CD=2AB=8.
点评:本题难度较大,考查相似三角形的判定和性质、三角形中位线定理.三角形的中位线平行于第三边,并且等于第三边的一半.

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
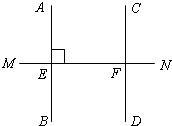 4、如图,已知AB⊥MN于E,下列条件中不能得到CD⊥MN的是( )
4、如图,已知AB⊥MN于E,下列条件中不能得到CD⊥MN的是( ) =∠BAP,AB=4,BP=x,CP=y,点C到MN的距离为线段CD的长.
=∠BAP,AB=4,BP=x,CP=y,点C到MN的距离为线段CD的长.
