Question

【题目】我们约定，在平面直角坐标系中两条抛物线有且只有一个交点时，我们称这两条抛物线为“郡园牵手抛物线”，这个交点为“郡园点”．例如：抛物线与是“郡园牵手抛物线”，“郡园点”为．

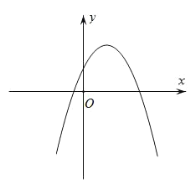
（1）如图，若抛物线与为“郡园牵手抛物线”，求的值；

（2）在（1）的条件下，若点是第一象限内抛物线上的动点，过作轴，为垂足，求的最大值；

（3）在（1）的条件下，设点是抛物线与的“郡园点”，点是抛物线上一动点，问在抛物线的对称轴上是否存在点，使是以点为直角顶点的等腰直角三角形？若存在，请直接写出点的坐标；若不存在，请说明理由．

Answer 1

【答案】（1）或4；（2）；（3）存在，符合条件的点有4个，．

【解析】

（1）根据题意得知与为“郡园牵手抛物线”，即只有一个交点，联立解析式解方程组即可得到答案； （2）由M是第一象限内的点可判断的解析式，设出用M的坐标，用M的坐标变量表示出，利用二次函数的性质求最大值即可 ； （3）根据题意画图并求出点B坐标为（-2，2），当抛物线分两种情况时依题意构造以C为直角顶点的等腰直角三角形，判断其大致图象，然后根据割补法构造全等三角形，再用待定系数法设出关键点的坐标，并表示出全等三角形边的长度，用对应边相等建立方程组求解即可．

解：（1）由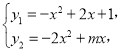可得：

，

∵只有一个交点，∴，

∴或4．

（2）∵点是第一象限内抛物线上的动点，∴，

设，其中，

则，

当时，有最大值，且最大值为．

（3）存在． 理由如下：

∵B是抛物线与的“郡园点”．

∴ 解得，，

把代入得，，

所以B点坐标为．

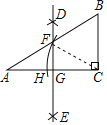
如图1，

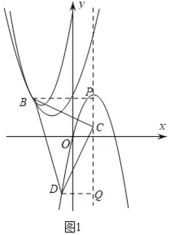
当抛物线 图象为时，

过B、D分别作BP、DQ垂直于抛物线对称轴直线，

依题意可设，且由图可得．

∵△BCD为等腰直角三角形，且C为直角顶点 ，

又∵∠CBP+∠BCP=90° ∴∠BCP+∠DCQ=90°，

在△BCP与△DCQ中，

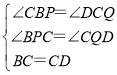
∴△BCP≌△DCQ（AAS） ∴BP=CQ，PC=DQ

即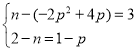

所以由得，代入得，，

整理得， ， 解得，（舍去），

此时C点坐标为．

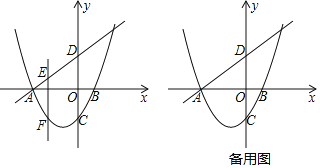
如图2，

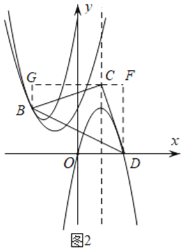
当抛物线图象为时，

过B、D分别作BG、DF分别平行于抛物线的对称轴直线，且过C作平行于轴的直线交BG于点G，交DF于点F．

依题意可设，且由图可得．

同理可证△BCG≌△CDF（AAS），所以CG=FD，BG=CF

即 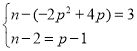解得，（舍去），

此时C点坐标为．

如图3，

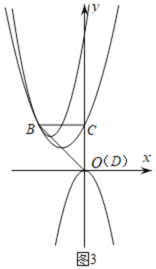
当抛物线图象为时，由△BCD是以C为直角顶点的等腰直角三角形可得BC=CD=2，此时D点与坐标原点O重合，C点坐标为．

如图4，

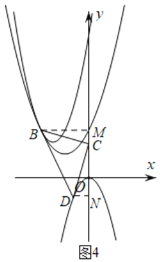
当抛物线图象为时，过B、D分别作BM、DN垂直于y轴交y轴于点M、N．由图可设．

同理易证△BCM≌△DCN（AAS） ∴BM=CN，MC=DN

即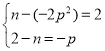 由得并代入得，

整理得，，

解得， ，

又∵当 时，过点C且垂直于BC的直线与抛物线没有交点，故此时D点不存在． ∴此时C点坐标为．

综上所述，满足题意的C点坐标可以为,,，．

所以存在,符合条件的点有4个，,,，．