题目内容
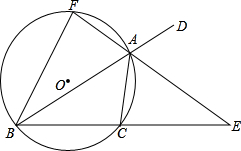
如图，点l是△ABC的内心，线段AI的延长线交△ABC外切圆于点D，交BC边于点E．
（1）求证：lD=BD．
（2）若
=
，lE=2，求AD的长．
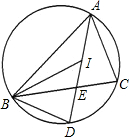
（1）求证：lD=BD．
（2）若
| BE |
| AB |
| 2 |
| 3 |
（1）证明：∵点I是△ABC的内心，
∴∠BAD=∠CAD，∠ABI=∠CBI
∴弧BD=弧CD，
∴∠DBC=∠CAD，
∴∠CBI+∠DBC=∠ABI+∠BAD，
∴∠CBI+∠DBC=∠DIB
即∠DBI=∠DIB，
∴ID=BD．
（2）∵∠DBC=∠CAD，
又∵∠BAD=∠CAD
∴∠DBC=∠BAD，
又∵∠BDE=∠ADB，
∴△BDE∽△ADB
∴
=
=
=
，
设DE=2a，则BD=3a，
则AD=
a
∵ID=BD，
∴IE=ID-DE=3a-2a=2，
∴a=2，
∴AD=9．
∴∠BAD=∠CAD，∠ABI=∠CBI
∴弧BD=弧CD，
∴∠DBC=∠CAD，
∴∠CBI+∠DBC=∠ABI+∠BAD，
∴∠CBI+∠DBC=∠DIB
即∠DBI=∠DIB，
∴ID=BD．
（2）∵∠DBC=∠CAD，
又∵∠BAD=∠CAD
∴∠DBC=∠BAD，
又∵∠BDE=∠ADB，
∴△BDE∽△ADB
∴
| DE |
| BD |
| BD |
| AD |
| BE |
| AB |
| 2 |
| 3 |
设DE=2a，则BD=3a，
则AD=
| 9 |
| 2 |
∵ID=BD，
∴IE=ID-DE=3a-2a=2，
∴a=2，
∴AD=9．
练习册系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
