题目内容
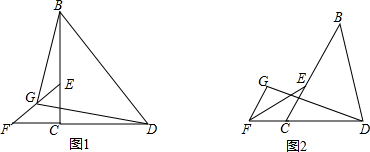
1.在△BCD中,点E在BC上,点F在DC的延长线上,且CE=CF,BC=DF,(1)如图1,当∠BCD=90°,G点为EF的中点时,连DG、BG,求证:BG⊥DG;
(2)如图2,当∠BCD=60°,FG∥CE,且FG=CE时,连接DG.求∠BDG的度数.
分析 (1)连接CG,根据等腰直角三角形的相关性质,结合邻补角可证∠BEG=∠DCG,进一步论证△BGE≌△DCG即可求解;
(2)连接CG,EG,BG,根据已知可证四边形GFCE是菱形,求出∠CGE=60°,∠ECG=60°,∠GCF=60°结合(1)中思路证明三角形全等即可求解.
解答 解:(1)如图1
连接CG,
由∠BCD=90°,G点为EF的中点,CE=CF易证:CG⊥EF,CG=GE,∠CEG=45°,∠GCF=45°,
∴∠BEG=∠DCG=135°,
∵CE=CF,BC=DF,
∴BE=CD,
在△BGE和△DCG中,$\left\{\begin{array}{l}{CG=GE}\\{∠BEG=∠DCG}\\{BE=CD}\end{array}\right.$,
∴△BGE≌△DCG,
∴∠DGC=∠BGE,
∴∠BGD=∠CGE=90°,
∴BG⊥DG.
(2)如图2
连接CG,EG,BG,
∵FG∥CE,且FG=CE,
∴四边形GFCE是平行四边形,
∵CF=CE,
∴平行四边形GFCE是菱形,
∴CE=EG,
由∠BCD=60°,可证三角形CGE为等边三角形,
∴∠CGE=60°,∠ECG=60°,∠GCF=60°,
∴∠BEG=∠DCG=120°,
在在△BGE和△DCG中,$\left\{\begin{array}{l}{CG=GE}\\{∠BEG=∠DCG}\\{BE=CD}\end{array}\right.$,
∴△BGE≌△DCG,
∴∠DGC=∠BGE,BG=GD,
∴∠BGD=∠CGE=60°,
∴三角形BGD为等边三角形,
∴∠BDG=60°.
点评 此题主要考查三角形和四边形的综合运用,熟悉三角形全等的证明,菱形的判定方法和性质的灵活运用;会推理等边三角形并适当运用是解题的关键.

 名校课堂系列答案
名校课堂系列答案| A. | (4,0) | B. | (0,0) | C. | (2,2$\sqrt{3}$) | D. | (4,$\sqrt{3}$) |
| A. | $\sqrt{6}$-3 | B. | -$\sqrt{6}$-3 | C. | 3-$\sqrt{6}$ | D. | $\frac{1}{\sqrt{6}-3}$ |
| A. | 3(x-1)-2(2x+3)=6 | B. | 3x-3-4x+3=1 | C. | 3(x-1)-2(2x+3)=1 | D. | 3x-3-4x-2=6 |
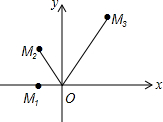 如图,在平面直角坐标系中,已知点M1(-1,0),将线段OM1绕点O按顺时针方向旋转60°,再将其长度伸长为OM1的2倍,得到线段OM2;又将线段OM2绕点O按顺时针方向旋转60°,长度伸长为OM2的2倍,得到线段OM3;如此下去,得到线段OM4,OM5…OMn(n为正整数),则点M234的坐标为(-2232,-2232•$\sqrt{3}$).
如图,在平面直角坐标系中,已知点M1(-1,0),将线段OM1绕点O按顺时针方向旋转60°,再将其长度伸长为OM1的2倍,得到线段OM2;又将线段OM2绕点O按顺时针方向旋转60°,长度伸长为OM2的2倍,得到线段OM3;如此下去,得到线段OM4,OM5…OMn(n为正整数),则点M234的坐标为(-2232,-2232•$\sqrt{3}$).