题目内容
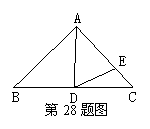
如图,在△ABC中,∠B=∠
C,∠BAD=40°,且∠ADE=∠AED,求∠CDE的度数.
 |
解:设∠DAE=x,则∠BAC=40°+x. 因为∠B=∠C,所以2∠2=180°-∠BAC,
∠C=90°-
∠BAC=90°-(40°+x). 同理∠AED=90°-∠DAE=90°
-x.
∠CDE=∠AED-∠C=(90°-x)-[90°-(40°+x)]=20°.
练习册系列答案
相关题目
题目内容
如图,在△ABC中,∠B=∠C,∠BAD=40°,且∠ADE=∠AED,求∠CDE的度数.
|
解:设∠DAE=x,则∠BAC=40°+x. 因为∠B=∠C,所以2∠2=180°-∠BAC,
∠C=90°-∠BAC=90°-(40°+x). 同理∠AED=90°-∠DAE=90°-x.
∠CDE=∠AED-∠C=(90°-x)-[90°-(40°+x)]=20°.
20、如图，在△ABC中，∠BAC=45°，现将△ABC绕点A逆时针旋转30°至△ADE的位置，使AC⊥DE，则∠B=
如图，在△ABC中，∠ACB=90°，AC=BC=1，取斜边的中点，向斜边作垂线，画出一个新的等腰三角形，如此继续下去，直到所画出的直角三角形的斜边与△ABC的BC重叠，这时这个三角形的斜边为
2、如图，在△ABC中，DE∥BC，那么图中与∠1相等的角是（ ）
如图，在△ABC中，AB=AC，且∠A=100°，∠B=