题目内容
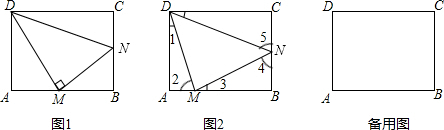
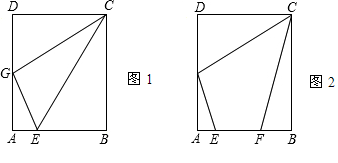
如图，D、E为△ABC边上的点，DE∥BC，
，△ADE的面积等于2，则四边形DBCE的面积等于
- A.8
- B.9
- C.16
- D.25
C
分析：根据题意，先求证△ADE∽△ABC，因为相似三角形的面积比是相似比的平方，则可得出S△ADE：S△ABC的比，则△ADE的面积：四边形DBCE的面积可求；已知△ADE的面积等于2，则四边形DBCE的面积可求．
解答：∵DE∥BC，
∴△ADE∽△ABC，
∵AD：AB=1：3，相似三角形的面积比是相似比的平方，
∴S△ADE：S△ABC=1：9，
∴△ADE的面积：四边形DBCE的面积=1：8，
又∵△ADE的面积等于2，
∴四边形DBCE的面积等于16．
故选C．
点评：本题主要考查相似三角形的判定及相似三角形的性质，要熟记相似三角形的面积比等于相似比的平方．
分析：根据题意，先求证△ADE∽△ABC，因为相似三角形的面积比是相似比的平方，则可得出S△ADE：S△ABC的比，则△ADE的面积：四边形DBCE的面积可求；已知△ADE的面积等于2，则四边形DBCE的面积可求．
解答：∵DE∥BC，
∴△ADE∽△ABC，
∵AD：AB=1：3，相似三角形的面积比是相似比的平方，
∴S△ADE：S△ABC=1：9，
∴△ADE的面积：四边形DBCE的面积=1：8，
又∵△ADE的面积等于2，
∴四边形DBCE的面积等于16．
故选C．
点评：本题主要考查相似三角形的判定及相似三角形的性质，要熟记相似三角形的面积比等于相似比的平方．
练习册系列答案
相关题目
19、如图，D、E为AB、AC的中点，将△ABC沿线段DE折叠，使点A落在点F处，若∠B=50°，则∠BDF=
