题目内容
如图，点D、E在△ABC的边BC上，AB=AC，AD=AE，且BD=4．求EC的长．分析：作AF⊥BC于点F，利用等腰三角形三线合一的性质得到BF=CF，DF=EF，相减后即可得到正确的结论．
解答：
证明：作AF⊥BC于点F，
∵AD=AE，AB=AC，
∴BF=CF，DF=EF，
∴BF-DF=CF-EF，
∴EC=BD=4．
证明：作AF⊥BC于点F，∵AD=AE，AB=AC，
∴BF=CF，DF=EF，
∴BF-DF=CF-EF，
∴EC=BD=4．
点评：考查了等腰三角形的性质，等腰三角形底边上的中线、底边上的高与顶角的平分线三线合一．
练习册系列答案
阅读快车系列答案
相关题目
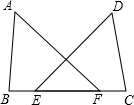如图，点E、F在BC上，AB=DC，∠B=∠C，∠A=∠D，
如图，点C、D在线段AB上，且C为AB的一个四等分点，D为AC中点，若BC=2，则BD的长为