题目内容
已知抛物线C1:y1=| 1 |
| 2 |
(I)求抛物线C1的顶点坐标;
(II)①若抛物线C1与y轴的交点为A,连接AF,并延长交抛物线C1于点B,求证:
| 1 |
| AF |
| 1 |
| BF |
②取抛物线C1上任意一点P(xP,yP)(0<xP<1),连接PF,并延长交抛物线C1于Q(xQ,yQ).试判断
| 1 |
| PF |
| 1 |
| QF |
(III)将抛物线C1作适当的平移,得抛物线C2:y2=
| 1 |
| 2 |
分析:(I)将抛物线C1:y1=
x2-x+1的一般式转化为顶点式,即可求得抛物线C1的顶点坐标;
(II)①由A(0,1),F(1,1),可得AB∥x轴,即可求得AF与BF的长,则问题得解;
②过点P(xp,yp)作PM⊥AB于点M,即可求得PF=yp,同理QF=yQ,然后由△PMF∽△QNF,根据相似三角形的对应边成比例,即可求得答案;
(III)令y3=x,设其图象与抛物线C2交点的横坐标为x0,x0′,且x0<x0′,观察图象,随着抛物线C2向右不断平移,x0,x0′的值不断增大,当满足2<x≤m,y2≤x恒成立时,m的最大值在x0′处取得.可得:当x0=2时,所对应的x0′即为m的最大值.
| 1 |
| 2 |
(II)①由A(0,1),F(1,1),可得AB∥x轴,即可求得AF与BF的长,则问题得解;
②过点P(xp,yp)作PM⊥AB于点M,即可求得PF=yp,同理QF=yQ,然后由△PMF∽△QNF,根据相似三角形的对应边成比例,即可求得答案;
(III)令y3=x,设其图象与抛物线C2交点的横坐标为x0,x0′,且x0<x0′,观察图象,随着抛物线C2向右不断平移,x0,x0′的值不断增大,当满足2<x≤m,y2≤x恒成立时,m的最大值在x0′处取得.可得:当x0=2时,所对应的x0′即为m的最大值.
解答:解:(I)∵y1=
x2-x+1=
(x-1)2+
,
∴抛物线C1的顶点坐标为(1,
);
(II)①证明:根据题意得:点A(0,1),
∵F(1,1),
∴AB∥x轴,得AF=BF=1,
∴
+
=2;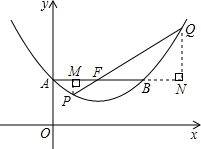
②
+
=2成立.
理由:
如图,过点P(xp,yp)作PM⊥AB于点M,
则FM=1-xp,PM=1-yp,(0<xp<1),
∴Rt△PMF中,由勾股定理,
得PF2=FM2+PM2=(1-xp)2+(1-yp)2,
又点P(xp,yp)在抛物线C1上,
得yp=
(xp-1)2+
,即(xp-1)2=2yp-1,
∴PF2=2yp-1+(1-yp)2=yp2,
即PF=yp,
过点Q(xQ,yQ)作QN⊥AB,与AB的延长线交于点N,
同理可得:QF=yQ,
∵∠PMF=∠QNF=90°,∠MFP=∠NFQ,
∴△PMF∽△QNF,
∴
=
,
这里PM=1-yp=1-PF,QN=yQ-1=QF-1,
∴
=
,
即
+
=2;
(III)令y3=x,
设其图象与抛物线C2交点的横坐标为x0,x0′,且x0<x0′,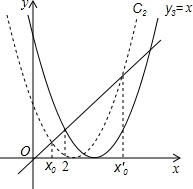
∵抛物线C2可以看作是抛物线y=
x2左右平移得到的,
观察图象,随着抛物线C2向右不断平移,x0,x0′的值不断增大,
∴当满足2<x≤m,y2≤x恒成立时,m的最大值在x0′处取得.
可得:当x0=2时,所对应的x0′即为m的最大值.
于是,将x0=2代入
(x-h)2=x,
有
(2-h)2=2,
解得:h=4或h=0(舍去),
∴y2=
(x-4)2.
此时,由y2=y3,得
(x-4)2=x,
解得:x0=2,x0′=8,
∴m的最大值为8.
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴抛物线C1的顶点坐标为(1,
| 1 |
| 2 |
(II)①证明:根据题意得:点A(0,1),
∵F(1,1),
∴AB∥x轴,得AF=BF=1,
∴
| 1 |
| AF |
| 1 |
| BF |

②
| 1 |
| PF |
| 1 |
| QF |
理由:
如图,过点P(xp,yp)作PM⊥AB于点M,
则FM=1-xp,PM=1-yp,(0<xp<1),
∴Rt△PMF中,由勾股定理,
得PF2=FM2+PM2=(1-xp)2+(1-yp)2,
又点P(xp,yp)在抛物线C1上,
得yp=
| 1 |
| 2 |
| 1 |
| 2 |
∴PF2=2yp-1+(1-yp)2=yp2,
即PF=yp,
过点Q(xQ,yQ)作QN⊥AB,与AB的延长线交于点N,
同理可得:QF=yQ,
∵∠PMF=∠QNF=90°,∠MFP=∠NFQ,
∴△PMF∽△QNF,
∴
| PF |
| QF |
| PM |
| QN |
这里PM=1-yp=1-PF,QN=yQ-1=QF-1,
∴
| PF |
| QF |
| 1-PF |
| QF-1 |
即
| 1 |
| PF |
| 1 |
| QF |
(III)令y3=x,
设其图象与抛物线C2交点的横坐标为x0,x0′,且x0<x0′,

∵抛物线C2可以看作是抛物线y=
| 1 |
| 2 |
观察图象,随着抛物线C2向右不断平移,x0,x0′的值不断增大,
∴当满足2<x≤m,y2≤x恒成立时,m的最大值在x0′处取得.
可得:当x0=2时,所对应的x0′即为m的最大值.
于是,将x0=2代入
| 1 |
| 2 |
有
| 1 |
| 2 |
解得:h=4或h=0(舍去),
∴y2=
| 1 |
| 2 |
此时,由y2=y3,得
| 1 |
| 2 |
解得:x0=2,x0′=8,
∴m的最大值为8.
点评:此题考查了二次函数的一般式与顶点式的转化,相似三角形的判定与性质以及最大值等问题.此题综合性很强,解题的关键是方程思想与数形结合思想的应用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 0)和点B.
0)和点B. 在平面直角坐标系xOy中,已知抛物线C1:y1=-x2+2x.
在平面直角坐标系xOy中,已知抛物线C1:y1=-x2+2x. 在平面直角坐标系xOy中,已知抛物线C1:y1=-x2+2x.
在平面直角坐标系xOy中,已知抛物线C1:y1=-x2+2x.