题目内容
【题目】如图,⊙O的直径AB=4,BC切⊙O于点B,OC平行于弦AD,OC=5,则AD的长为( ) 
A.![]()
B.![]()
C.![]()
D.![]()
【答案】B
【解析】解:连接BD. ∵AB是直径,∴∠ADB=90°.
∵OC∥AD,∴∠A=∠BOC,∴cos∠A=cos∠BOC.
∵BC切⊙O于点B,∴OB⊥BC,
∴cos∠BOC= ![]() =
= ![]() ,
,
∴cos∠A=cos∠BOC= ![]() .
.
又∵cos∠A= ![]() ,AB=4,
,AB=4,
∴AD= ![]() .
.
故选B.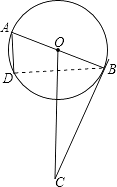
首先由切线的性质得出OB⊥BC,根据锐角三角函数的定义求出cos∠BOC的值;连接BD,由直径所对的圆周角是直角,得出∠ADB=90°,又由平行线的性质知∠A=∠BOC,则cos∠A=cos∠BOC,在直角△ABD中,由余弦的定义求出AD的长.

练习册系列答案
相关题目









