题目内容
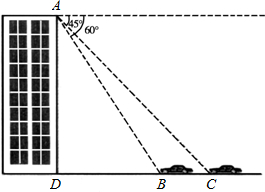
(2012•建邺区一模)如图,某同学在大楼30m高的窗口看地面上两辆汽车B、C,测得俯角分别为60°和45°,如果汽车B、C在与该楼的垂直线上行使,求汽车C与汽车B之间的距离.(精确到0.1m,参考数据:
≈1.414,
≈1.732)
| 2 |
| 3 |

分析:在直角△ADC和直角△ADB中,利用三角函数即可求得CD、BD的长,根据BC=CD-BD即可求解.
解答:解:依题意得,∠ACD=45°,∠ABD=60°
Rt△ADC中,
=tan45°,
∴CD=
=
=30(m).
Rt△ADB中,
=tan60°,
∴BD=
=10
(m).
∴BC=30-10
≈12.7(m).
答:汽车C与汽车B之间的距离约为12.7m.
Rt△ADC中,
| AD |
| CD |
∴CD=
| AD |
| tan45° |
| 30 |
| 1 |
Rt△ADB中,
| AD |
| BD |
∴BD=
| AD |
| tan60° |
| 3 |
∴BC=30-10
| 3 |
答:汽车C与汽车B之间的距离约为12.7m.
点评:本题考查俯角的定义,能正确利用三角函数定义,解直角三角形是关键.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
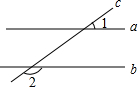 (2012•建邺区一模)如图,直线a、b被第三条直线c所截,且a∥b,若∠1=35°,则∠2=
(2012•建邺区一模)如图,直线a、b被第三条直线c所截,且a∥b,若∠1=35°,则∠2= 从点B出发沿BC方向以每秒1个单位的速度向点C运动,设运动时间为t秒.
从点B出发沿BC方向以每秒1个单位的速度向点C运动,设运动时间为t秒. (2012•建邺区一模)如图,矩形ABCD中,A(-4,1),B(0,1),C(0,3),则D点坐标是
(2012•建邺区一模)如图,矩形ABCD中,A(-4,1),B(0,1),C(0,3),则D点坐标是