题目内容
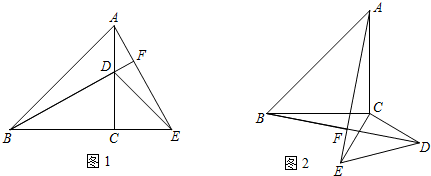
如图1,已知△ABC与△DCE都是等腰直角三角形,AC=BC,DC=EC,∠ACB=∠DCE=90°,点D在AC上,直线BD交AE于点F.
(1)请补充完整证明“BD=AE,BF⊥AE”的推理过程;
证明:在△ACE与△BCD中
∵(________)
∴△ACE≌△BCD(SAS)
∴BD=AE,∠CAE=∠CBD(全等三角形的对应角相等)
∵∠ACE=90°
∴∠CAE+∠AEC=90°(________)
∴∠CBD+∠AEC=90°(等量代换)
∴________
∴BF⊥AE(垂直的定义)
(2)将△DCE绕着点C旋转,在旋转过程中保持△DCE的大小与形状均不变,那么,当△DCE旋转至图2的位置时,(1)中的结论是否仍然成立?为什么?
(1)证明:∵在△ACE和△BCD中
 ,
,
∴△ACE≌△BCD(SAS),
∴BD=AE,∠CAE=∠CBD,
∵∠ACE=90°,
∴∠CAE+∠AEC=90°(直角三角形的两锐角互余),
∴∠BFE=90°,
∴BF⊥AE,
故答案为:AC=BC,∠DCB=∠ECA,CE=CD,直角三角形的两锐角互余,∠BFE=90°.
(2)解:(1)中的结论还成立,
理由是:∵∠ACB=∠DCE=90°,
∴∠ACB+∠BCE=∠DCE+∠BCE,
∴∠ACE=∠BCD,
在△ACE和△BCD中
 ,
,
∴△ACE≌△BCD(SAS),
∴BD=AE,∠CAE=∠CBD,
∵∠ACE=90°,
∴∠CAE+∠AHC=90°,
∵∠AHC=∠BHF,∠HBF=∠CAH,
∴∠BHF+∠HBF=90°
∴∠BFE=90°,
∴BF⊥AE.
分析:(1)根据SAS证△ACE≌△BCD,推出BD=AE,∠CAE=∠CBD,根据∠ACE=90°求出∠CAE+∠AEC=90°,推出∠BFE=90°,根据垂直定义推出即可;
(2)求出∠ACE=∠BCD,其余证明过程和(1)类似.
点评:本题考查了全等三角形的性质和判定,垂直定义,三角形的内角和定理等知识点的应用,注意:全等三角形的对应边相等,对应角相等,全等三角形的判定定理有SAS,ASA,AAS,SSS.
 ,
,∴△ACE≌△BCD(SAS),
∴BD=AE,∠CAE=∠CBD,
∵∠ACE=90°,
∴∠CAE+∠AEC=90°(直角三角形的两锐角互余),
∴∠BFE=90°,
∴BF⊥AE,
故答案为:AC=BC,∠DCB=∠ECA,CE=CD,直角三角形的两锐角互余,∠BFE=90°.
(2)解:(1)中的结论还成立,
理由是:∵∠ACB=∠DCE=90°,
∴∠ACB+∠BCE=∠DCE+∠BCE,
∴∠ACE=∠BCD,
在△ACE和△BCD中
 ,
,∴△ACE≌△BCD(SAS),
∴BD=AE,∠CAE=∠CBD,

∵∠ACE=90°,
∴∠CAE+∠AHC=90°,
∵∠AHC=∠BHF,∠HBF=∠CAH,
∴∠BHF+∠HBF=90°
∴∠BFE=90°,
∴BF⊥AE.
分析:(1)根据SAS证△ACE≌△BCD,推出BD=AE,∠CAE=∠CBD,根据∠ACE=90°求出∠CAE+∠AEC=90°,推出∠BFE=90°,根据垂直定义推出即可;
(2)求出∠ACE=∠BCD,其余证明过程和(1)类似.
点评:本题考查了全等三角形的性质和判定,垂直定义,三角形的内角和定理等知识点的应用,注意:全等三角形的对应边相等,对应角相等,全等三角形的判定定理有SAS,ASA,AAS,SSS.

练习册系列答案
 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
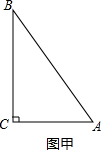 定义:若某个图形可分割为若干个都与他相似的图形,则称这个图形是自相似图形.
定义:若某个图形可分割为若干个都与他相似的图形,则称这个图形是自相似图形.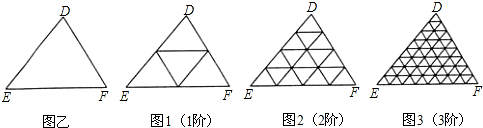
 如图,若已知△ABC中,D、E分别为AB、AC的中点,则可得DE∥BC,且DE=
如图,若已知△ABC中,D、E分别为AB、AC的中点,则可得DE∥BC,且DE=

