题目内容
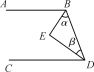
【题目】在矩形ABCD中，AB=4，AD=6，M是AD边的中点，P是射线AB上的一个动点（不与A，B重合），MN⊥PM交射线BC于N点．
（1）如图1，当点N与点C重合时，求AP的长；
（2）如图2，在点N的运动过程中，求证： 
为定值；
（3）在射线AB上，是否存在点P，使得△DCN∽△PMN？若存在，求此时AP的长；若不存在，请说明理由．
【答案】
（1）
解：∵矩形ABCD，∴∠A=∠D=90°，
∵MN⊥PM，
∴∠APM=90°﹣∠AMP=∠DMC，
∴△APM∽△DMC，
∴ 
= 
，
∵点M是AD的中点，
∴MD=AM= 
AD=3，
∵CD=AB=4，
∴ 
= 
，
∴AP= 
（2）
解：证明：①当点P在线段AB上时，如图2，
延长MN交DC的延长线于G，
同（1）的方法得出，△APM∽△DMG，
∴ 
= 
，
∴ = 
= 
，
∴ 
+ 
= 
+ 
，
∵AD∥CN，
∴∠CNG=∠DMG=∠APM，
∵∠PAM=∠NCG=90°，
∴△APM∽△CNG，
∴ 
，
∴ = ，
∴ = ，
∴ 
= ；
②当点P在AB的延长线上时，如图，
同①的方法得出，△APM∽△DMH，
∴ 
，
∴ 
，
∴ 
，
∴ 
，
∴ 
，
同①的方法得出，△APM∽△CNH，
∴ 
，
∴ 
，
∴ = ；
即： 
是定值
（3）
解：存在点P，使得△DCN∽△PMN，
解：由（2）知 = ，△DCN∽△PMN时，
∴ 
= ，
∴ 
= ，
∴CN=4，
易得，△MDH∽△NCH，
∴ 
= 
. = ，
∵CD=AB=4，
∴DH= 
，CH= 
，
由（2）②知，△APM∽△MDH，
∴ = 
，
∴ = 
，
P= 
【解析】（1）先判断出∠APM=∠DMC即可得出△APM∽△DMC，即 = ，再求出AM=MD=3，CD=4代入即可；（2）分两种情况①判断出，△APM∽△DMG，和△APM∽△CNG用得出的比例式化简即可得出结论；②同①的方法即可得出结论；（3）先求出CN，再用△MDH∽△NCH求出DH，CH，最后用△APM∽△MDH即可求出结论．
