题目内容
某种消费品每件60元,不收附加税时,每年大约销售80万件,若政府收附加税时,每销售100元要征税x元(叫做税率x%),则每年销售量将减少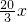 万件,要使每年在此项经营中收取的税金不少于128万元,问税率x%的范围是________,当税率x%=________时,所收取的税金最多,为________万元.
万件,要使每年在此项经营中收取的税金不少于128万元,问税率x%的范围是________,当税率x%=________时,所收取的税金最多,为________万元.
4%≤x%≤8% 6% 144
分析:依题意,征税后销量为80- x万件价格不变,税率为x%,销售额乘以税率即为所征附加税额,令其大于128既得满足条件的不等式,解出x的范围,再利用二次函数的最值得出最大值即可.
x万件价格不变,税率为x%,销售额乘以税率即为所征附加税额,令其大于128既得满足条件的不等式,解出x的范围,再利用二次函数的最值得出最大值即可.
解答:依题意有:征附加税x元(叫做税率x%),则每年销售量将减少 x万件,则销量变为(80-
x万件,则销量变为(80- x)万件,
x)万件,
要使每年在此项经营中所收取的附加税额不少于128万元,则可以建立如下不等式:
(80- x)×100×
x)×100× ≥128,
≥128,
解得:4≤x≤8.
∴4%≤x%≤8%,
W=(80- x)×100×
x)×100× ,
,
=- x2+80x,
x2+80x,
当x=- =-
=- =6时,
=6时,
W最大= =144,
=144,
故答案为:4%≤x%≤8%,6%,144.
点评:此题主要考查了二次函数的应用,本题是函数模型的简单应用,借助函数模型考查一元二次不等式的解法,是基础题.
分析:依题意,征税后销量为80-
 x万件价格不变,税率为x%,销售额乘以税率即为所征附加税额,令其大于128既得满足条件的不等式,解出x的范围,再利用二次函数的最值得出最大值即可.
x万件价格不变,税率为x%,销售额乘以税率即为所征附加税额,令其大于128既得满足条件的不等式,解出x的范围,再利用二次函数的最值得出最大值即可.解答:依题意有:征附加税x元(叫做税率x%),则每年销售量将减少
 x万件,则销量变为(80-
x万件,则销量变为(80- x)万件,
x)万件,要使每年在此项经营中所收取的附加税额不少于128万元,则可以建立如下不等式:
(80-
 x)×100×
x)×100× ≥128,
≥128,解得:4≤x≤8.
∴4%≤x%≤8%,
W=(80-
 x)×100×
x)×100× ,
,=-
 x2+80x,
x2+80x,当x=-
 =-
=- =6时,
=6时,W最大=
 =144,
=144,故答案为:4%≤x%≤8%,6%,144.
点评:此题主要考查了二次函数的应用,本题是函数模型的简单应用,借助函数模型考查一元二次不等式的解法,是基础题.

练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案
相关题目