题目内容
如图,正方形ABCD的边长为a,在AB、BC、CD、DA边上分别取点A1、B1、C1、D1,使AA1=BB1=CC1=DD1= a,在边A1B1、B1C1、C1D1、D1A1上分别取点A2、B2、C2、D2,使A1A2=B1B2=C1C2=D1D2=
a,在边A1B1、B1C1、C1D1、D1A1上分别取点A2、B2、C2、D2,使A1A2=B1B2=C1C2=D1D2=
 A1B2,….依次规律继续下去,则正方形AnBnCnDn的面积为 .
A1B2,….依次规律继续下去,则正方形AnBnCnDn的面积为 .

 : 解:在Rt△A1BB1中,由勾股定理可知;
: 解:在Rt△A1BB1中,由勾股定理可知; =
= =
= ,即正方形A1B1C1D1的面积=
,即正方形A1B1C1D1的面积= ;
;
在Rt△A2B1B2中,由勾股定理可知: =
= =
= ;即正方形A2B2C2D2的面积=
;即正方形A2B2C2D2的面积=
…
∴正方形AnBnCnDn的面积= .
.

练习册系列答案
 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案 全优冲刺100分系列答案
全优冲刺100分系列答案
相关题目
一个批发商销售成本为 20元/千克的某产品,根据物价部门规定:该产品每千克售价不得超过90元,在销售过程中发现的售量y(千克)与售价x(元/千克)满足一次函数关系,对应关系如下表:
20元/千克的某产品,根据物价部门规定:该产品每千克售价不得超过90元,在销售过程中发现的售量y(千克)与售价x(元/千克)满足一次函数关系,对应关系如下表:
| 售价x(元/千克) | … | 50 | 60 | 70 | 80 | … |
| 销售量y(千克) | … | 100 | 90 | 80 | 70 | … |
(1)求y与x的函数关系式;
(2)该批发商若想获得4000元的利润,应将售价定为多少元?
(3)该产品每千克售价为多少元时,批发商获得的利润w(元)最大?此时的最大利润为多少元?
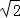 =1.41,
=1.41,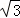 =1.73).
=1.73).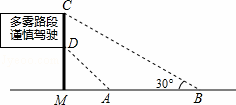

 B.
B.  C.
C.  D.
D. 
 . (3,1) C. (﹣3,1) D. (﹣1,3)
. (3,1) C. (﹣3,1) D. (﹣1,3)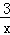 的图象上.
的图象上. .线段AB的中垂线与线段AC的中垂线的交点
.线段AB的中垂线与线段AC的中垂线的交点 图4
图4